June 2024, Week 3: June 10th - June 16th

June 10 -> 1051. Height Checker

A school is trying to take an annual photo of all the students. The students are asked to stand in a single file line in non-decreasing order by height. Let this ordering be represented by the integer array expected where expected[i] is the expected height of the ith student in line.

You are given an integer array heights representing the current order that the students are standing in. Each heights[i] is the height of the ith student in line (0-indexed).

Return the number of indices where heights[i] != expected[i].

Example 1:

Input: heights = [1,1,4,2,1,3]
Output: 3
Explanation:
- heights: [1,1,4,2,1,3]
- expected: [1,1,1,2,3,4]
- Indices 2, 4, and 5 do not match.

Example 2:

Input: heights = [5,1,2,3,4]
Output: 5
Explanation:
- heights: [5,1,2,3,4]
- expected: [1,2,3,4,5]
- All indices do not match.

Example 3:

Input: heights = [1,2,3,4,5]
Output: 0
Explanation:
- heights: [1,2,3,4,5]
- expected: [1,2,3,4,5]
- All indices match.

Constraints:

1 <= heights.length <= 100
1 <= heights[i] <= 100

Approach 1: Counting Sort and Comparison

def heightChecker1(heights: List[int]) -> int: """ Determines the number of mismatched positions between the current and expected height order of students. This function implements a solution using counting sort to create the expected height order. It first creates a copy of the input list and sorts it using a custom counting sort algorithm. Then, it compares the original list with the sorted list to count mismatches. The time complexity of this solution is O(n + k), where `n` is the number of students and `k` is the range of heights. This is because counting sort takes O(n + k) time, and the final comparison takes O(n) time. The space complexity is O(n + k) due to the additional list for sorted heights and the frequency map used in counting sort. """ def counting_sort(heights_list: List[int]) -> None: """ Helper function to perform counting sort on the given list of heights in-place. """ frequency_map = defaultdict(int) for height in heights_list: frequency_map[height] += 1 min_height, max_height = min(heights_list), max(heights_list) sorted_index = 0 for height in range(min_height, max_height + 1): for _ in range(frequency_map[height]): heights_list[sorted_index] = height sorted_index += 1 expected_heights = heights[:] counting_sort(expected_heights) mismatch_count = 0 for current_height, expected_height in zip(heights, expected_heights): if current_height != expected_height: mismatch_count += 1 return mismatch_count

Understanding the Core Idea

The central concept of this solution is to leverage counting sort to efficiently create the expected order of student heights, then compare it with the original order to count mismatches. This approach exploits the limited range of heights specified in the problem constraints.

Counting Sort Application: Utilizes counting sort, which is particularly effective for sorting integers with a known, limited range.
In-Place Sorting: Applies the sorting algorithm to a copy of the original list, preserving the initial order for comparison.
Direct Comparison: Performs a straightforward comparison between the original and sorted lists to count mismatches.

Code Walkthrough

Counting Sort Helper Function:
def counting_sort(heights_list: List[int]) -> None: frequency_map = defaultdict(int) for height in heights_list: frequency_map[height] += 1
This helper function implements counting sort. It starts by creating a frequency map of heights, which is efficient due to the limited range of possible heights. Using defaultdict simplifies the code by automatically initializing counts to zero.
Sorting Process:
min_height, max_height = min(heights_list), max(heights_list) sorted_index = 0 for height in range(min_height, max_height + 1): for _ in range(frequency_map[height]): heights_list[sorted_index] = height sorted_index += 1
This part of the counting sort algorithm reconstructs the sorted list in-place. It iterates through the possible height range, placing each height in the correct position based on its frequency. This approach is efficient as it only needs to iterate through the actual range of heights present in the list. It first determines the minimum and maximum heights to define the range of values to consider, then fills in the sorted list based on the frequency of each height.
Creating and Sorting Expected Heights:
expected_heights = heights[:] counting_sort(expected_heights)
A copy of the original heights list is created and then sorted using the counting sort algorithm. This step creates the expected order of heights without modifying the original list.
Counting Mismatches:
mismatch_count = 0 for current_height, expected_height in zip(heights, expected_heights): if current_height != expected_height: mismatch_count += 1
This loop compares the original heights with the sorted heights, incrementing the mismatch count for each difference. Using zip allows for a clean, parallel iteration over both lists.
Returning Result:
return mismatch_count
The function returns the total number of mismatches, which represents the number of students not in their correct height order.

Complexity Analysis

Time Complexity:

, where is the number of students, and is the range of possible heights.
- Counting the frequency of heights:
- Reconstructing the sorted list:
- Comparing original and sorted lists: This is because the counting sort algorithm runs in linear time with respect to the number of elements and the range of values, and the final comparison is a linear scan of the lists.

Space Complexity:

, where is the number of students, and is the range of possible heights.
- Copy of the original list:
- Frequency map in counting sort: The space complexity is dominated by the need to store a copy of the original list and the frequency map used in the counting sort algorithm.

Example

Input:

heights = [1, 2, 6, 4, 2, 5]

Step-by-Step Walkthrough:

Initialization:
- The function heightChecker1 is called with the input list heights = [1, 2, 6, 4, 2, 5].
- A copy of heights is created as expected_heights = [1, 2, 6, 4, 2, 5].
Counting Sort Process:
- A frequency_map is created using a defaultdict(int):
  - Here each height is mapped to its frequency (frequency_map = {1: 1, 2: 2, 6: 1, 4: 1, 5: 1}).
- The min_height (1) and max_height (6) are determined.
- The sorting process begins, iterating from min_height to max_height:
  - Height 1: Placed at index 0
  - Height 2: Placed at indices 1 and 2
  - Height 3: Skipped (frequency is 0)
  - Height 4: Placed at index 3
  - Height 5: Placed at index 4
  - Height 6: Placed at index 5
- After sorting, expected_heights becomes [1, 2, 2, 4, 5, 6]
Comparison and Mismatch Counting:
- The function compares heights with expected_heights:
  - Index 0: 1 == 1 (Match)
  - Index 1: 2 == 2 (Match)
  - Index 2: 6 != 2 (Mismatch, count = 1)
  - Index 3: 4 == 4 (Match)
  - Index 4: 2 != 5 (Mismatch, count = 2)
  - Index 5: 5 != 6 (Mismatch, count = 3)
Visual Aids:
- Comparison Summary Table:
  Index
  Current Height
  Expected Height
  Status
  0
  1
  1
  Match
  1
  2
  2
  Match
  2
  6
  2
  Mismatch
  3
  4
  4
  Match
  4
  2
  5
  Mismatch
  5
  5
  6
  Mismatch
- Visual Representation of Mismatches:
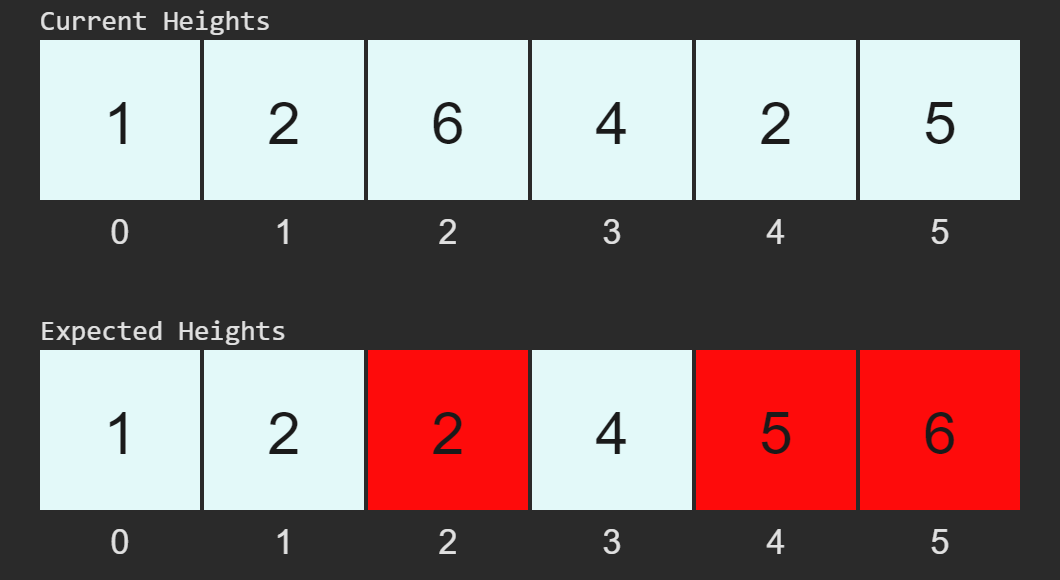
Result Calculation:
- The final mismatch count is 3, which is the number of indices where heights[i] != expected_heights[i].
- This count represents the number of students who are not in their correct positions based on height.

Index	Current Height	Expected Height	Status
0	1	1	Match
1	2	2	Match
2	6	2	Mismatch
3	4	4	Match
4	2	5	Mismatch
5	5	6	Mismatch

Example

...

Last modified: 10 July 2024