July 2024 Weekly Exercises

Week 1 -> 1101. The Earliest Moment When Everyone Becomes Friends

There are n people in a social group labeled from 0 to n - 1. You are given an array logswhere logs[i] = [timestamp_i, x_i, y_i] indicates that x_i and y_i will be friends at the time timestamp_i.

Friendship is symmetric. That means if a is friends with b, then b is friends with a. Also, person a is acquainted with a person b if a is friends with b, or a is a friend of someone acquainted with b.

Return the earliest time for which every person became acquainted with every other person. If there is no such earliest time, return -1.

Example 1:

Input: logs = [[20190101,0,1],[20190104,3,4],[20190107,2,3],[20190211,1,5],[20190224,2,4],[20190301,0,3],[20190312,1,2],[20190322,4,5]], n = 6
Output: 20,190,301
Explanation:
- The first event occurs at timestamp = 20,190,101, and after 0 and 1 become friends, we have the following friendship groups [0,1], [2], [3], [4], [5].
- The second event occurs at timestamp = 20,190,104, and after 3 and 4 become friends, we have the following friendship groups [0,1], [2], [3,4], [5].
- The third event occurs at timestamp = 20,190,107, and after 2 and 3 become friends, we have the following friendship groups [0,1], [2,3,4], [5].
- The fourth event occurs at timestamp = 20,190,211, and after 1 and 5 become friends, we have the following friendship groups [0,1,5], [2,3,4].
- The fifth event occurs at timestamp = 20,190,224, and as 2 and 4 are already friends, nothing happens.
- The sixth event occurs at timestamp = 20,190,301, and after 0 and 3 become friends, we all become friends.

Example 2:

Input: logs = [[0,2,0],[1,0,1],[3,0,3],[4,1,2],[7,3,1]], n = 4
Output: 3
Explanation: At timestamp = 3, all the persons (i.e., 0, 1, 2, and 3) become friends.

Constraints:

2 <= n <= 100
1 <= logs.length <= 10^4
logs[i].length == 3
0 <= timestamp_i <= 10^9
0 <= x_i, y_i <= n - 1
x_i != y_i
All the values timestamp_i are unique.
All the pairs (x_i, y_i) occur at most one time in the input.

Approach 1: Approach Name

def earliestAcq1(logs: List[List[int]], n: int) -> int: """ Determines the earliest time when all people in a social group become acquainted. This function uses the Union-Find data structure to efficiently track friend connections and group formations. It sorts the logs by timestamp and processes each friendship event chronologically. The algorithm leverages the properties of the Union-Find structure to quickly check if all individuals have become part of a single connected component. The time complexity of this solution is O(m log m + n + m * α(n)), where 'm' is the number of logs, 'n' is the number of people and α(n) is the inverse Ackermann function. This is due to the initial sort operation (O(m log m)), the UnionFind initialization (O(n)) and for each log (m), we call the union operation which uses union by rank and calls find twice. Its time complexity is amortized O(α(n)). The space complexity is O(m + n), accounting for the sorted logs and the UnionFind data structure. """ if len(logs) < n - 1: return -1 # Not enough friendships to connect all people logs.sort(key=lambda x: x[0]) # Sort logs by timestamp friend_network_uf = UnionFind(n) for timestamp, person_a, person_b in logs: friend_network_uf.union(person_a, person_b) if friend_network_uf.is_single_component(): return timestamp # All people are connected return -1

class UnionFind: """ Implements the Union-Find data structure with path compression and union by rank optimizations. """ def __init__(self, size: int, offset: int = 0): """ Initializes the Union-Find data structure with the given number of elements and optional offset. """ self.root = [i for i in range(size + offset)] self.rank = [1] * (size + offset) self.num_components = size def find(self, x: int) -> int: """ Finds the root of the set containing x, applying path compression for efficiency. """ if x == self.root[x]: return x self.root[x] = self.find(self.root[x]) return self.root[x] def union(self, x: int, y: int) -> bool: """ Unites the sets containing x and y if they are not already in the same set. Returns True if a new union was performed, False otherwise. """ root_x = self.find(x) root_y = self.find(y) if root_x == root_y: return False if self.rank[root_x] < self.rank[root_y]: self.root[root_x] = root_y else: self.root[root_y] = root_x if self.rank[root_x] == self.rank[root_y]: self.rank[root_x] += 1 self.num_components -= 1 return True def is_single_component(self) -> bool: """Checks if all elements are in a single set.""" return self.num_components == 1

Understanding the Core Idea

The central concept of this solution is to leverage the Union-Find data structure to efficiently track friend connections and group formations in a dynamic social network. This approach allows us to quickly determine when all individuals become part of a single connected component.

Chronological Processing: By sorting the logs by timestamp, we ensure that friendships are processed in the order they occur, allowing us to pinpoint the exact moment when full connectivity is achieved.
Union-Find Efficiency: The Union-Find data structure provides near-constant time operations for joining sets (making friendships) and checking if all elements are in a single set (full connectivity).
Early Termination: The algorithm can stop as soon as full connectivity is detected, avoiding unnecessary processing of later friendship logs.

Code Walkthrough

Initial Validation:
if len(logs) < n - 1: return -1 # Not enough friendships to connect all people
This check ensures that there are at least enough friendship logs to potentially connect all people. If not, we can immediately return -1 as it's impossible to achieve full connectivity. This is a graph theory concept where a connected graph with n nodes must have at least n - 1 edges.
Sorting Logs:
logs.sort(key=lambda x: x[0]) # Sort logs by timestamp
Sorting the logs by timestamp is crucial as it allows us to process friendships in chronological order. This is necessary to find the earliest time of full connectivity. We only need to consider the order of friendships, not the specific people involved; hence, we sort by x[0].
Initializing Union-Find:
friend_network_uf = UnionFind(n)
We initialize a Union-Find data structure with n elements, representing each person in the social network. This structure will efficiently track friend groups as they form and merge.
Processing Friendships:
for timestamp, person_a, person_b in logs: friend_network_uf.union(person_a, person_b) if friend_network_uf.is_single_component(): return timestamp # All people are connected
We iterate through the sorted logs, performing two key operations for each friendship:
- union(person_a, person_b): This merges the sets containing person_a and person_b, effectively forming or expanding a friend group.
- is_single_component(): After each union, we check if all people are now in a single component. If so, we've found the earliest time of full connectivity and can return the current timestamp.
Final Check:
return -1
If we've processed all logs without achieving full connectivity, we return -1 to indicate that it's not possible with the given friendships.

Complexity Analysis

Time Complexity:

, where is the number of logs, is the number of people, and is the inverse Ackermann function.
- Sorting the logs takes time.
- Initializing the Union-Find structure takes time.
- Processing each log involves a union operation, which has an amortized time complexity of due to path compression and union by rank optimizations.
- The factor grows extremely slowly and is effectively constant for all practical values of , so the overall complexity is often simplified to .

Space Complexity:

, where is the number of logs and is the number of people.
- The sorted logs array requires space.
- The Union-Find data structure uses space to store the parent array and rank information for each person.

Example

Input:

logs = [[0, 2, 0], [1, 0, 1], [3, 0, 3], [4, 1, 2], [7, 3, 1]]
n = 4

Step-by-Step Walkthrough:

Initialization:
- The function earliestAcq1 is called with logs and n = 4 as arguments.
- We first check if there are enough friendship logs to potentially connect all people:
  if len(logs) < n - 1: return -1
  In this case, len(logs) = 5 and n - 1 = 3, so we continue.
Sorting Logs:
- The logs list is sorted based on the timestamp (first element of each sublist):
  logs.sort(key=lambda x: x[0])
- After sorting, logs becomes:
  [[0, 2, 0], [1, 0, 1], [3, 0, 3], [4, 1, 2], [7, 3, 1]]
Initializing Union-Find:
- A UnionFind object is created with n = 4 elements:
  friend_network_uf = UnionFind(n)
- This creates four disjoint sets, one for each person (0, 1, 2, 3).
- Here is a visual representation of the initial state:
Main Loop (Processing Friendships):
- Iteration 1:
  - Timestamp: 0, Person A: 2, Person B: 0
  - friend_network_uf.union(2, 0) is called
  - This operation merges the sets containing 2 and 0
  - Here is the updated state after the first iteration:
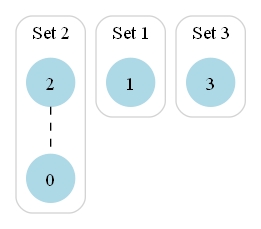
  - is_single_component() returns False (not all people are connected yet)
- Iteration 2:
  - Timestamp: 1, Person A: 0, Person B: 1
  - friend_network_uf.union(0, 1) is called
  - This operation merges the sets containing 0 (which now includes 2) and 1
  - Here is the updated state after the second iteration:
  - is_single_component() returns False (person 3 is still not connected)
- Iteration 3:
  - Timestamp: 3, Person A: 0, Person B: 3
  - friend_network_uf.union(0, 3) is called
  - This operation merges the sets containing 0 (which now includes 1 and 2) and 3
  - Here is the updated state after the third iteration:
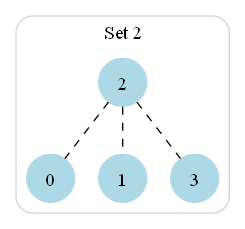
  - is_single_component() returns True (all people are now connected)
  - The function returns the current timestamp: 3
Loop Termination:
- The loop terminates after the third iteration because all people are connected.
- The remaining friendship logs (timestamps 4 and 7) are not processed.
Visual Aids: Iteration Summary Table:
Iteration
Timestamp
Person A
Person B
Union Result
Is Single Component
1
0
2
0
True
False
2
1
0
1
True
False
3
3
0
3
True
True
Result Calculation/Final Steps:
- The function returns the timestamp 3, which is the earliest time when all people became acquainted.
- This is because at timestamp 3, the last person (person 3) was connected to the group containing all other people (0, 1, and 2).

Iteration	Timestamp	Person A	Person B	Union Result	Is Single Component
1	0	2	0	True	False
2	1	0	1	True	False
3	3	0	3	True	True

Complexity Analysis

...

Example

...

Last modified: 06 July 2024