July 2024, Week 1: July 1st - July 7th
July 1 -> 1550. Three Consecutive Odds
Given an integer arr, return true if there are three consecutive odd numbers in the array. Otherwise, return false.
Example 1:
Input: arr = [2,6,4,1] Output: false Explanation: There are no three consecutive odds.
Example 2:
Input: arr = [1,2,34,3,4,5,7,23,12] Output: true Explanation: [5,7,23] are three consecutive odds.
Constraints:
1 <= arr.length <= 10001 <= arr[i] <= 1000
Approach 1: Single-Pass Counter
Understanding the Core Idea
The central concept of this solution is to leverage a single-pass iteration with a counter to efficiently detect three consecutive odd numbers in the array. This approach exploits the sequential nature of the problem and the binary property of numbers (odd or even).
Counter Reset Mechanism: The solution uses a counter that increments for odd numbers and resets for even numbers, allowing it to track consecutive odd numbers efficiently.
Early Termination: The algorithm returns
Trueas soon as it detects three consecutive odd numbers, avoiding unnecessary iterations through the rest of the array.
Code Walkthrough
Input Validation:
if len(arr) < 3: return FalseThis check ensures that the array has at least three elements. If not, it's impossible to have three consecutive odd numbers, so we return
Falseimmediately. This optimization prevents unnecessary processing for small arrays.Counter Initialization:
consecutive_odds = 0We initialize a counter
consecutive_oddsto keep track of the number of consecutive odd integers encountered. This single variable is key to the algorithm's space efficiency.Array Iteration and Odd Number Detection:
for num in arr: if num % 2: consecutive_odds += 1 else: consecutive_odds = 0We iterate through each number in the array. The modulo operation
num % 2checks if a number is odd (remainder 1 when divided by 2). If it's odd, we increment the counter. If it's even, we reset the counter to 0. This reset is crucial as it ensures we're only counting consecutive odd numbers.Consecutive Odd Check and Early Return:
if consecutive_odds == 3: return TrueAfter each update to
consecutive_odds, we check if it has reached 3. If so, we've found three consecutive odd numbers, and we can immediately returnTrue. This early return optimizes the function by avoiding unnecessary iterations once the condition is met.Final Return:
return FalseIf we've iterated through the entire array without finding three consecutive odd numbers, we return
False.
Complexity Analysis
Time Complexity:
, where is the length of the input array arr. This is because in the worst case, we need to iterate through all elements of the array once. Each operation inside the loop (modulo, increment, comparison) takes constant time, so the overall time complexity is linear with respect to the array length.
Space Complexity:
, or constant space. This is because we only use a single integer variable consecutive_oddsregardless of the input size. The space used does not grow with the size of the input array, making this solution very memory-efficient.
Example
Input:
Step-by-Step Walkthrough:
Initialization:
The function
threeConsecutiveOdds1is called with the input array[1, 2, 34, 3, 4, 5, 7, 23, 12].The variable
consecutive_oddsis initialized to 0. This variable will keep track of the count of consecutive odd numbers encountered.
Input Validation:
The function checks if the length of the input array is less than 3.
In this case, the array length is 9, which is valid (greater than or equal to 3), so the function proceeds.
Main Loop:
Iteration 1:
Current number: 1
1 is odd (1 % 2 = 1), so
consecutive_oddsis incremented to 1.1 < 3, so the function continues to the next iteration.
Iteration 2:
Current number: 2
2 is even (2 % 2 = 0), so
consecutive_oddsis reset to 0.
Iteration 3:
Current number: 34
34 is even (34 % 2 = 0), so
consecutive_oddsremains 0.
Iteration 4:
Current number: 3
3 is odd (3 % 2 = 1), so
consecutive_oddsis incremented to 1.
Iteration 5:
Current number: 4
4 is even (4 % 2 = 0), so
consecutive_oddsis reset to 0.
Iteration 6:
Current number: 5
5 is odd (5 % 2 = 1), so
consecutive_oddsis incremented to 1.
Iteration 7:
Current number: 7
7 is odd (7 % 2 = 1), so
consecutive_oddsis incremented to 2.
Iteration 8:
Current number: 23
23 is odd (23 % 2 = 1), so
consecutive_oddsis incremented to 3.At this point,
consecutive_oddsequals 3, so the function immediately returnsTrue.
Visual Aid:
The iteration summary table shows the progression of the
consecutive_oddscount for each element in the array.
Element
Number
Odd/Even
Consecutive Odds
1
1
Odd
1
2
2
Even
0
3
34
Even
0
4
3
Odd
1
5
4
Even
0
6
5
Odd
1
7
7
Odd
2
8
23
Odd
3
Result Calculation/Final Steps:
The function returns
Trueas soon as it encounters three consecutive odd numbers (5, 7, 23).The last element (12) is not processed because the function has already found the desired pattern and returned.
July 2 -> 350. Intersection of Two Arrays II
Given two integer arrays nums1 and nums2, return an array of their intersection. Each element in the result must appear as many times as it shows in both arrays, and you may return the result in any order.
Example 1:
Input: nums1 = [1,2,2,1], nums2 = [2,2]
Output: [2,2]
Example 2:
Input: nums1 = [4,9,5], nums2 = [9,4,9,8,4]
Output: [4,9]
Explanation: [9,4] is also accepted.
Constraints:
1 <= nums1.length, nums2.length <= 10000 <= nums1[i], nums2[i] <= 1000
Approach 1: Two-Pointer on Sorted Arrays
Understanding the Core Idea
The central concept of this solution is to leverage sorted arrays and a two-pointer technique to efficiently find the intersection of two integer arrays while maintaining element frequency. This approach exploits the ordered nature of sorted arrays to compare elements linearly and identify common elements.
Sorting: By sorting both input arrays, we create a structure where identical elements are grouped together, making comparisons easier.
Two-Pointer Technique: Using two pointers, one for each sorted array, we can traverse both arrays simultaneously, comparing elements and identifying matches.
Frequency Preservation: The algorithm naturally preserves the frequency of elements in the intersection by including a match in the result each time it occurs in both arrays.
Code Walkthrough
Array Swapping for Optimization:
if len(nums1) > len(nums2): nums1, nums2 = nums2, nums1This step ensures that
nums1is always the shorter (or equal length) array. This optimization can reduce space complexity in cases where one array is significantly shorter than the other.Sorting the Arrays:
nums1.sort() nums2.sort()Sorting both arrays is crucial for the two-pointer approach to work. It allows us to compare elements sequentially and efficiently identify matches.
Initialization:
intersection = [] index1, index2 = 0, 0We initialize an empty list
intersectionto store the result, and two pointersindex1andindex2to traversenums1andnums2respectively.Two-Pointer Traversal:
while index1 < len(nums1) and index2 < len(nums2): if nums1[index1] < nums2[index2]: index1 += 1 elif nums1[index1] > nums2[index2]: index2 += 1 else: intersection.append(nums1[index1]) index1 += 1 index2 += 1This is the core of the algorithm. We compare elements from both arrays:
If the element in
nums1is smaller, we move theindex1pointer.If the element in
nums2is smaller, we move theindex2pointer.If they are equal, we've found an intersection element. We add it to the result and move both pointers. This process naturally handles frequency, as we only add an element when we find a match in both arrays.
Result Return:
return intersectionAfter the traversal,
intersectioncontains all common elements with their correct frequencies, so we return it.
Complexity Analysis
Time Complexity:
, where and are the lengths of nums1andnums2respectively. This is because:Sorting both arrays takes
and time. The two-pointer traversal is linear,
. The sorting step dominates the time complexity.
Space Complexity:
, where and are the lengths of nums1andnums2. This is because:The result array
intersectionwill at most contain as many elements as the shorter input array.The space used for sorting (which could be
or for Python's built-in sort) is not counted as extra space in this analysis, as it's considered part of the input modification. Apart from the result array, we only use a constant amount of extra space for pointers and temporary variables.
Example
Input:
Step-by-Step Walkthrough:
Initialization:
The function first checks if
nums1is longer thannums2. In this case,len(nums1) = 3andlen(nums2) = 5, so no swap occurs.Both arrays are then sorted:
nums1becomes[4, 5, 9]nums2becomes[4, 4, 8, 9, 9]
Initialize
intersection = [],index1 = 0, andindex2 = 0
Main Loop (Two-pointer comparison):
Iteration 1:
Compare
nums1[0] = 4andnums2[0] = 4They are equal, so add 4 to
intersectionIncrement both
index1andindex2Current state:
intersection = [4],index1 = 1,index2 = 1
Iteration 2:
Compare
nums1[1] = 5andnums2[1] = 45 > 4, so increment onlyindex2Current state:
intersection = [4],index1 = 1,index2 = 2
Iteration 3:
Compare
nums1[1] = 5andnums2[2] = 85 < 8, so increment onlyindex1Current state:
intersection = [4],index1 = 2,index2 = 2
Iteration 4:
Compare
nums1[2] = 9andnums2[2] = 89 > 8, so increment onlyindex2Current state:
intersection = [4],index1 = 2,index2 = 3
Iteration 5:
Compare
nums1[2] = 9andnums2[3] = 9They are equal, so add 9 to
intersectionIncrement both
index1andindex2Current state:
intersection = [4, 9],index1 = 3,index2 = 4
Loop Termination:
After iteration 5,
index1 = 3, which equalslen(nums1), so the loop terminatesThe final state of variables:
intersection = [4, 9]index1 = 3index2 = 4
Visual Aid:
Iteration Summary Table:
Iteration
index1
index2
nums1 value
nums2 value
Action
Current Intersection
1
0
0
4
4
Add to intersection, increment both
[4]
2
1
1
5
4
Increment index2
[4]
3
1
2
5
8
Increment index1
[4]
4
2
2
9
8
Increment index2
[4]
5
2
3
9
9
Add to intersection, increment both
[4, 9]
Result Calculation/Final Steps:
The algorithm has already built the intersection array during the loop iterations
No further calculations are needed
The function returns the final
intersectionarray:[4, 9]
Approach 2: Hash Table (Counter) Approach
Understanding the Core Idea
The central concept of this solution is to leverage a hash table (specifically, Python's Counter class) to efficiently find the intersection of two integer arrays while maintaining element frequency. This approach exploits the
Hash Table Usage: By creating a frequency map of the shorter array, we can quickly check for the presence of elements and their remaining counts.
Single Pass through Longer Array: We only need to iterate through the longer array once, checking each element against the frequency map.
Frequency Preservation: The algorithm naturally preserves the frequency of elements in the intersection by decrementing the count in the frequency map each time a match is found.
Code Walkthrough
Array Swapping for Optimization:
if len(nums1) > len(nums2): nums1, nums2 = nums2, nums1This step ensures that
nums1is always the shorter (or equal length) array. This optimization reduces space complexity by creating the frequency map for the smaller array.Creating the Frequency Map:
count_nums1 = Counter(nums1)We use Python's
Counterclass to create a frequency map ofnums1. This hash-based data structure allows foraverage-case lookups and updates. Initialization of Result Array:
intersection = []We initialize an empty list
intersectionto store the common elements.Iterating through the Longer Array:
for num in nums2: if count_nums1[num] > 0: intersection.append(num) count_nums1[num] -= 1This is the core of the algorithm. For each number in
nums2:We check if it exists in
count_nums1and has a count greater than 0.If it does, we add it to the
intersectionlist and decrement its count incount_nums1. This process naturally handles frequency, as we only add an element when it's still available in the frequency map.
Result Return:
return intersectionAfter the iteration,
intersectioncontains all common elements with their correct frequencies, so we return it.
Complexity Analysis
Time Complexity:
, where and are the lengths of nums1andnums2respectively. This is because:Creating the
Counterfornums1takestime. Iterating through
nums2takestime. Each lookup and update in the
Counterison average.
Space Complexity:
, where and are the lengths of nums1andnums2. This is because:The
Counterwill contain at most as many elements as the shorter input array (which we ensure isnums1).The result array
intersectionwill also contain at most as many elements as the shorter input array.By swapping arrays if necessary, we guarantee that we're using the minimum possible space for the
Counter.
Example
Input:
Step-by-Step Walkthrough:
Initialization:
The function first checks if
nums1is longer thannums2. In this case,len(nums1) = 3andlen(nums2) = 5, so no swap occurs.Create a Counter object
count_nums1fromnums1:count_nums1 = Counter({4: 1, 9: 1, 5: 1})Initialize
intersection = []
Main Loop (Iterating through nums2):
Iteration 1:
Processing
num = 9count_nums1[9] = 1, which is > 0Add 9 to
intersectionDecrement
count_nums1[9]to 0Current state:
intersection = [9]
Iteration 2:
Processing
num = 4count_nums1[4] = 1, which is > 0Add 4 to
intersectionDecrement
count_nums1[4]to 0Current state:
intersection = [9, 4]
Iteration 3:
Processing
num = 9count_nums1[9] = 0, which is not > 0No action taken
Current state:
intersection = [9, 4]
Iteration 4:
Processing
num = 8count_nums1[8] = 0(default for a missing key), which is not > 0No action taken
Current state:
intersection = [9, 4]
Iteration 5:
Processing
num = 4count_nums1[4] = 0, which is not > 0No action taken
Current state:
intersection = [9, 4]
Loop Termination:
The loop terminates after processing all elements in
nums2The final state of variables:
intersection = [9, 4]count_nums1 = Counter({4: 0, 9: 0, 5: 1})
Visual Aid:
Iteration Summary Table:
Iteration
Number
Count after action
Action
Current Intersection
1
9
0
Add 9 to intersection, decrement count
[9]
2
4
0
Add 4 to intersection, decrement count
[9, 4]
3
9
0
No action
[9, 4]
4
8
0
No action
[9, 4]
5
4
0
No action
[9, 4]
Result Calculation/Final Steps:
The algorithm has already built the intersection array during the loop iterations
No further calculations are needed
The function returns the final
intersectionarray:[9, 4]
July 3 -> 1509. Minimum Difference Between Largest and Smallest Value in Three Moves
You are given an integer array nums.
In one move, you can choose one element of nums and change it to any value.
Return the minimum difference between the largest and smallest value of nums after performing at most three moves.
Example 1:
Input: nums = [5,3,2,4]
Output: 0
Explanation: We can make at most 3 moves.
In the first move, change 2 to 3. nums becomes [5,3,3,4].
In the second move, change 4 to 3. nums becomes [5,3,3,3].
In the third move, change 5 to 3. nums becomes [3,3,3,3].
After performing 3 moves, the difference between the minimum and maximum is 3 - 3 = 0.
Example 2:
Input: nums = [1,5,0,10,14]
Output: 1
Explanation: We can make at most 3 moves.
In the first move, change 5 to 0. nums becomes [1,0,0,10,14].
In the second move, change 10 to 0. nums becomes [1,0,0,0,14].
In the third move, change 14 to 1. nums becomes [1,0,0,0,1].
After performing 3 moves, the difference between the minimum and maximum is 1 - 0 = 1. It can be shown that there is no way to make the difference 0 in 3 moves.
Example 3:
Input: nums = [3,100,20]
Output: 0
Explanation: We can make at most 3 moves.
In the first move, change 100 to 7. nums becomes [3,7,20].
In the second move, change 20 to 7. nums becomes [3,7,7].
In the third move, change 3 to 7. nums becomes [7,7,7].
After performing three moves, the difference between the minimum and maximum is 7 - 7 = 0.
Constraints:
1 <= nums.length <= 10^5-10^9 <= nums[i] <= 10^9
Approach 1: Greedy Optimization with Heap Operations
Understanding the Core Idea
The central concept of this solution is to leverage heap operations to efficiently identify the elements that have the most significant impact on the range of the array. By focusing on the four smallest and four largest elements, we can explore all possible combinations of three moves that minimize the difference between the maximum and minimum values.
Edge Case Handling: The solution first addresses the scenario where the array has 4 or fewer elements, recognizing that in this case, all elements can be made equal.
Extrema Extraction: Using heap operations, the algorithm efficiently extracts the four smallest and four largest elements from the array.
Optimal Move Combination: By considering all possible ways to apply three moves to these extreme elements, the solution determines the minimal achievable difference.
Code Walkthrough
Edge Case Handling:
if len(nums) <= 4: return 0This check addresses the scenario where we have four or fewer elements. In such cases, we can always make all elements equal using at most three moves, resulting in a minimum difference of 0.
Extrema Extraction:
smallest_four = heapq.nsmallest(4, nums) largest_four = heapq.nlargest(4, nums)Here, we use heap operations to efficiently extract the four smallest and four largest elements from the input array. These elements are crucial because they represent the boundaries of our possible solutions after applying up to three moves.
Optimal Move Calculation:
return min( largest_four[0] - smallest_four[3], # Change 3 smallest largest_four[1] - smallest_four[2], # Change 2 smallest, 1 largest largest_four[2] - smallest_four[1], # Change 1 smallest, 2 largest largest_four[3] - smallest_four[0] # Change 3 largest )This step calculates and compares four scenarios, each representing a different way to apply the three allowed moves:
Change the 3 smallest elements: We compare the largest element with the 4th smallest.
Change 2 smallest and 1 largest: We compare the 2nd largest with the 3rd smallest.
Change 1 smallest and 2 largest: We compare the 3rd largest with the 2nd smallest.
Change the 3 largest elements: We compare the 4th largest with the smallest element.
By taking the minimum of these four scenarios, we find the smallest possible difference achievable with at most three moves.
Complexity Analysis
Time Complexity:
, where is the number of elements in the input array nums. This is because bothheapq.nsmallest()andheapq.nlargest()operations have a time complexity of, where is 4 in our case. Since is a constant, this simplifies to . The final min()operation is performed on a constant number of elements, so it doesn't affect the overall time complexity.
Space Complexity:
, because we only store a constant number of elements (8 in total: 4 smallest and 4 largest) regardless of the input size. The space used does not grow with the input size, making it constant space complexity.
Example
Input:
Step-by-Step Walkthrough:
Initialization:
The function starts by initializing
nas the length of the input listnums.n = len(nums) = 8
Edge Case Check:
The function checks if
n <= 4. In this case,n = 8, so this condition is false, and we proceed with the main algorithm.
Extracting Smallest and Largest Elements:
The function uses
heapq.nsmallest(4, nums)to find the four smallest elements:[0, 4, 5, 6]It then uses
heapq.nlargest(4, nums)to find the four largest elements:[21, 10, 8, 7]These operations efficiently extract the extremes without fully sorting the list.
Calculating Possible Differences:
The function calculates four different scenarios, each representing a different strategy for applying the three allowed moves:
Iteration 1 (Change 3 smallest):
Largest:
21(largest element)Smallest:
6(4th smallest element)Difference:
21 - 6 = 15
Iteration 2 (Change 2 smallest, 1 largest):
Largest:
10(2nd largest element)Smallest:
5(3rd smallest element)Difference:
10 - 5 = 5
Iteration 3 (Change 1 smallest, 2 largest):
Largest:
8(3rd largest element)Smallest:
4(2nd smallest element)Difference:
8 - 4 = 4
Iteration 4 (Change 3 largest):
Largest:
7(4th largest element)Smallest:
0(smallest element)Difference:
7 - 0 = 7
Visual Aid - Difference Summary:
Strategy
Largest
Smallest
Difference
Change 3 smallest
21
6
15
Change 2 smallest, 1 largest
10
5
5
Change 1 smallest, 2 largest
8
4
4
Change 3 largest
7
0
7
Finding Minimum Difference:
The function identifies the minimum difference from the calculated scenarios:
4The corresponding strategy is "Change 1 smallest, 2 largest."
Result Calculation/Final Steps:
The minimum difference
4is returned as the final result.This result represents the smallest possible difference between the maximum and minimum elements in the array after applying at most three moves.
In this case, the optimal strategy would be to change the smallest element and the two largest elements, resulting in a final array where the difference between the largest and smallest elements is 4.
July 4 -> 2181. Merge Nodes in Between Zeros
You are given the head of a linked list, which contains a series of integers separated by 0's. The beginning, and end of the linked list will have Node.val == 0.
For every two consecutive 0's, merge all the nodes lying in between them into a single node whose value is the sum of all the merged nodes. The modified list should not contain any 0's.
Return the head of the modified linked list.
Example 1:

Input: head = [0,3,1,0,4,5,2,0]
Output: [4,11]
Explanation: The above figure represents the given linked list. The modified list contains
The sum of the nodes marked in green: 3 + 1 = 4.
The sum of the nodes marked in red: 4 + 5 + 2 = 11.
Example 2:

Input: head = [0,1,0,3,0,2,2,0]
Output: [1,3,4]
Explanation: The above figure represents the given linked list. The modified list contains
The sum of the nodes marked in green: 1 = 1.
The sum of the nodes marked in red: 3 = 3.
The sum of the nodes marked in yellow: 2 + 2 = 4.
Constraints:
The number of nodes in the list is in the range
[3, 2 * 10^5].0 <= Node.val <= 1000There are no two consecutive nodes with
Node.val == 0.The beginning and end of the linked list have
Node.val == 0.
Approach 1: Two-Pointer Traversal with In-Place Modification
Understanding the Core Idea
The central concept of this solution is to use two pointers to traverse the linked list while simultaneously modifying it in-place. This approach allows us to merge nodes between zeros efficiently without creating a new list.
Two-Pointer Technique: The solution uses two pointers:
result_nodefor building the modified list andtraversal_nodefor iterating through the original list.In-Place Modification: Instead of creating a new list, the solution modifies the existing list, which saves space and simplifies the process.
Running Sum: A
current_sumvariable is used to accumulate the sum of values between zeros.
Code Walkthrough
Initialization:
result_node = head traversal_node = head.next_node current_sum = 0We initialize
result_nodeto the head (which is a zero node),traversal_nodeto the next node to start processing, andcurrent_sumto zero. This setup allows us to start summing from the first non-zero node.Traversal and Summing:
while traversal_node: if traversal_node.val == 0: result_node = result_node.next_node result_node.val = current_sum current_sum = 0 else: current_sum += traversal_node.val traversal_node = traversal_node.next_nodeThis is the core of the algorithm. We traverse the list with
traversal_node, summing values until we hit a zero. When we encounter a zero:We move
result_nodeto the next node (which will store our sum)We set its value to the accumulated sum
We reset
current_sumfor the next group If the current node is not zero, we simply add its value tocurrent_sum.
Finalizing the List:
result_node.next_node = None return head.next_nodeAfter the traversal, we set the
next_nodeof the last result node toNone, effectively trimming any remaining nodes. We returnhead.next_nodebecause the original head was a zero node that we don't want in our final list.
Complexity Analysis
Time Complexity:
, where is the number of nodes in the original linked list. This is because we traverse the list exactly once, performing constant-time operations at each node.
Space Complexity:
, as we are modifying the list in-place and only using a constant amount of extra space for our pointers and the current_sumvariable, regardless of the input size.
Example
Input:
A visual representation of the input linked list:

Step-by-Step Walkthrough:
Initialization:
result_nodeis set to the head of the list (value 0)traversal_nodeis set to the next node (value 3)current_sumis initialized to 0
Main Loop (Merging nodes between zeros):
Iteration 1:
Current state:
result_node.val = 0,traversal_node.val = 3,current_sum = 0The traversal node is not 0, so we add its value to
current_sumcurrent_sumbecomes 3Move
traversal_nodeto the next node
Iteration 2:
Current state:
result_node.val = 0,traversal_node.val = 1,current_sum = 3The traversal node is not 0, so we add its value to
current_sumcurrent_sumbecomes 4Move
traversal_nodeto the next node
Iteration 3:
Current state:
result_node.val = 0,traversal_node.val = 0,current_sum = 4The traversal node is 0, triggering the merging process:
Move
result_nodeto the next nodeSet
result_node.valto the current sum (4)Reset
current_sumto 0
The list is updated:

Move
traversal_nodeto the next node
Iteration 4:
Current state:
result_node.val = 4,traversal_node.val = 4,current_sum = 0The traversal node is not 0, so we add its value to
current_sumcurrent_sumbecomes 4Move
traversal_nodeto the next node
Iteration 5:
Current state:
result_node.val = 4,traversal_node.val = 5,current_sum = 4The traversal node is not 0, so we add its value to
current_sumcurrent_sumbecomes 9Move
traversal_nodeto the next node
Iteration 6:
Current state:
result_node.val = 4,traversal_node.val = 2,current_sum = 9The traversal node is not 0, so we add its value to
current_sumcurrent_sumbecomes 11Move
traversal_nodeto the next node
Iteration 7:
Current state:
result_node.val = 4,traversal_node.val = 0,current_sum = 11The traversal node is 0, triggering the merging process:
Move
result_nodeto the next nodeSet
result_node.valto the current sum (11)Reset
current_sumto 0
The list is updated:

Move
traversal_nodeto the next node
Loop Termination:
The loop terminates when
traversal_nodebecomes None, indicating we've reached the end of the list
Final List Adjustment:
Set
result_node.next_nodeto None, effectively removing any remaining nodes
Visual Aid: Iteration Summary:
Iteration
Result Node Val
Traversal Node Val
Current Sum
Action
1
0
1
3
Added 3 to sum
2
0
0
4
Added 1 to sum
3
4
4
0
Zero found, sum applied
4
4
5
4
Added 4 to sum
5
4
2
9
Added 5 to sum
6
4
0
11
Added 2 to sum
7
11
None
0
Zero found, sum applied
Result Calculation/Final Steps:
The function returns
head.next_node, which is the start of the merged listThe output list is [4, 11]
A visual representation of the output linked list:
July 5 -> 2058. Find the Minimum and Maximum Number of Nodes Between Critical Points
A critical point in a linked list is defined as either a local maxima or a local minima.
A node is a local maxima if the current node has a value strictly greater than the previous node and the next node.
A node is a local minima if the current node has a value strictly smaller than the previous node and the next node.
Note that a node can only be a local maxima/minima if there exists both a previous node and a next node.
Given a linked list head, return an array of length 2 containing [minDistance, maxDistance] where minDistance is the minimum distance between any two distinct critical points and maxDistance is the maximum distance between any two distinct critical points. If there are fewer than two critical points, return [-1, -1].
Example 1:
Input: head = [3,1] Output: [-1,-1] Explanation: There are no critical points in [3,1].
Example 2:

Input:
head = [5,3,1,2,5,1,2]Output:
[1,3]Explanation: There are three critical points:
The third node is a local minima because 1 is less than 3 and 2.
The fifth node is a local maxima because 5 is greater than 2 and 1.
The sixth node is a local minima because 1 is less than 5 and 2.
The minimum distance is between the fifth and the sixth node. minDistance = 6 - 5 = 1.
The maximum distance is between the third and the sixth node. maxDistance = 6 - 3 = 3.
Example 3:

Input:
head = [1,3,2,2,3,2,2,2,7]Output:
[3,3]Explanation: There are two critical points:
The second node is a local maxima because 3 is greater than 1 and 2.
The fifth node is a local maxima because 3 is greater than 2 and 2.
Both the minimum and maximum distances are between the second and the fifth node. Thus, minDistance and maxDistance are 5 - 2 = 3. Note that the last node is not considered a local maxima because it does not have a next node.
Constraints:
The number of nodes in the list is in the range
[2, 10^5].1 <= Node.val <= 10^5
Approach 1: Single-Pass Traversal with Sliding Window
Understanding the Core Idea
The central concept of this solution is to leverage a single-pass traversal with a sliding window of three nodes to identify critical points in a linked list. This approach allows for efficient detection of local maxima and minima while simultaneously calculating the minimum and maximum distances between these critical points.
Sliding Window: The algorithm uses a three-node window (previous, current, and next) that slides through the linked list, allowing for local comparisons to identify critical points.
Critical Point Detection: By comparing the values of three consecutive nodes, the algorithm can determine if the current node is a local maximum or minimum.
Distance Tracking: The solution keeps track of the first and last critical points, as well as the minimum distance between any two adjacent critical points.
Code Walkthrough
Initial Check and Initialization:
if not head.next_node.next_node: return [-1, -1] prev_node = head current_node = head.next_node first_critical_index, last_critical_index = None, None min_distance = float('inf') current_index = 1The function first checks if the list has at least three nodes, as required for a critical point. It then initializes variables to keep track of the previous and current nodes, the indices of the first and last critical points, and the minimum distance between critical points.
Main Loop - Traversing the List:
while current_node.next_node: current_index += 1 # Check if we have a critical point if ( # Local maxima prev_node.val < current_node.val > current_node.next_node.val # Local minima or prev_node.val > current_node.val < current_node.next_node.val ):This loop traverses the list, incrementing the
current_indexfor each node. It checks if the current node is a critical point by comparing it with its previous and next nodes. A critical point is identified if the current node is a local maxima or minima.Critical Point Processing:
if not first_critical_index: first_critical_index = current_index else: min_distance = min(min_distance, current_index - last_critical_index) last_critical_index = current_indexWhen a critical point is found, the code updates the
first_critical_indexif it's the first one encountered. For later critical points, it updates themin_distanceby comparing it with the distance to the last critical point. Thelast_critical_indexis always updated to the current index.Window Sliding:
prev_node = current_node current_node = current_node.next_nodeAt the end of each iteration, the window slides forward by updating the
prev_nodeandcurrent_node.Result Calculation and Return:
if min_distance != float('inf'): max_distance = last_critical_index - first_critical_index return [min_distance, max_distance] return [-1, -1]After the traversal, if at least two critical points were found (
min_distancewas updated), the function calculates themax_distanceas the difference between the last and first critical point indices. It returns these values as a list. If fewer than two critical points were found, it returns[-1, -1]as specified in the problem statement.
Complexity Analysis
Time Complexity:
, where is the number of nodes in the linked list. This is because the algorithm performs a single pass through the entire linked list, processing each node exactly once.
Space Complexity:
, as the algorithm uses only a constant amount of extra space regardless of the input size. It maintains a fixed number of variables ( prev_node,current_node,first_critical_index,last_critical_index,min_distance,current_index) throughout the execution, and does not use any data structures that grow with the input size.
Example
Input:
A visual representation of the input linked list:

Step-by-Step Walkthrough:
Initialization:
We start by checking if the linked list has at least three nodes. In this case, it does, so we proceed.
Initialize variables:
prev_node = head(value: 5)current_node = head.next_node(value: 3)first_critical_index = Nonelast_critical_index = Nonemin_distance = float('inf')current_index = 1
Main Loop:
Iteration 1:
current_indexis incremented to 2Current state:
prev_node= 5,current_node= 3,next_node= 1Check if we have a critical point:
Local maxima: 5 < 3 > 1? No
Local minima: 5 > 3 < 1? No
Not a critical point, so we move to the next iteration
Update:
prev_node = 3,current_node = 1
Iteration 2:
current_indexis incremented to 3Current state:
prev_node= 3,current_node= 1,next_node= 2Check if we have a critical point:
Local maxima: 3 < 1 > 2? No
Local minima: 3 > 1 < 2? Yes
Critical point found (local minima)
Set
first_critical_index = 3Set
last_critical_index = 3Update:
prev_node = 1,current_node = 2
Iteration 3:
current_indexis incremented to 4Current state:
prev_node= 1,current_node= 2,next_node= 5Check if we have a critical point:
Local maxima: 1 < 2 > 5? No
Local minima: 1 > 2 < 5? No
Not a critical point, so we move to the next iteration
Update:
prev_node = 2,current_node = 5
Iteration 4:
current_indexis incremented to 5Current state:
prev_node= 2,current_node= 5,next_node= 1Check if we have a critical point:
Local maxima: 2 < 5 > 1? Yes
Critical point found (local maxima)
Update
min_distancesince this is not the first critical point:min_distance = min(inf, 5 - 3) = 2
Update
last_critical_index = 5Update:
prev_node = 5,current_node = 1
Iteration 5:
current_indexis incremented to 6Current state:
prev_node= 5,current_node= 1,next_node= 2Check if we have a critical point:
Local maxima: 5 > 1 < 2? No
Local minima: 5 < 1 < 2? Yes
Critical point found (local minima)
Update
min_distance:min_distance = min(2, 6 - 5) = 1
Update
last_critical_index = 6Update:
prev_node = 1,current_node = 2
Loop Termination:
The loop terminates as
current_node.next_nodeisNoneFinal state of variables:
first_critical_index = 3last_critical_index = 6min_distance = 1
Visual Aids:
Iteration Summary:
Node Index
Prev
Current
Next
Is Critical
First Critical
Last Critical
Min Distance
2
5
3
1
False
inf
3
3
1
2
True
3
3
inf
4
1
2
5
False
3
3
inf
5
2
5
1
True
3
5
2
6
5
1
2
True
3
6
1
Here is a visual representation of the critical points:

Result Calculation/Final Steps:
We found at least two critical points, so we proceed to calculate the result
Calculate
max_distance:max_distance = last_critical_index - first_critical_index = 6 - 3 = 3
The final result is
[min_distance, max_distance] = [1, 3]
This result means:
The minimum distance between any two distinct critical points is 1 (between indices 5 and 6)
The maximum distance between any two distinct critical points is 3 (between indices 3 and 6)
July 6 -> 2582. Pass the Pillow
There are n people standing in a line labeled from 1 to n. The first person in the line is holding a pillow initially. Every second, the person holding the pillow passes it to the next person standing in the line. Once the pillow reaches the end of the line, the direction changes, and people continue passing the pillow in the opposite direction.
For example, once the pillow reaches the
nthperson, they pass it to then - 1thperson, then to then - 2thperson and so on.
Given the two positive integers n and time, return the index of the person holding the pillow after time seconds.
Example 1:
Input:
n = 4, time = 5Output: 2
Explanation: People pass the pillow in the following way: 1 -> 2 -> 3 -> 4 -> 3 -> 2.
After five seconds, the second person is holding the pillow.
Example 2:
Input:
n = 3, time = 2Output: 3
Explanation: People pass the pillow in the following way: 1 -> 2 -> 3.
After two seconds, the third person is holding the pillow.
Constraints:
2 <= n <= 10001 <= time <= 1000
Approach 1: Modular Arithmetic with Cycle Detection
Understanding the Core Idea
The central concept of this solution is to leverage modular arithmetic to efficiently calculate the pillow's position without simulating the entire process. This approach exploits the cyclic nature of the pillow's movement.
Cycle Length Calculation: The solution recognizes that the pillow's movement forms a complete cycle every
2(n-1)seconds, wherenis the number of people.Position within Cycle: By using the modulo operation, the solution determines the position within a single cycle, avoiding the need to iterate through all time steps.
Direction Determination: The solution uses a simple comparison to determine whether the pillow is moving forward or backward within the cycle.
Code Walkthrough
Cycle Position Calculation:
cycle_position = time % ((n - 1) * 2)This line calculates the position within a single back-and-forth cycle.
(n - 1) * 2represents the total time for one complete cycle (forward and backward). The modulo operation%gives us the remainder, which is the position within the current cycle.Direction and Position Determination:
if cycle_position < n: return cycle_position + 1 else: return 2 * n - (cycle_position + 1)This conditional block determines the direction of the pillow's movement and calculates its position:
If
cycle_position < n, the pillow is moving forward. The position is simplycycle_position + 1(adding 1 because people are labeled from 1 to n, not 0 to n-1).Otherwise, the pillow is moving backward. The calculation
2 * n - (cycle_position + 1)determines the position by considering the total path length (2n) and subtracting the current progress (cycle_position + 1).
Result Return: The function implicitly returns the calculated position, which represents the index of the person holding the pillow after the given time.
Complexity Analysis
Time Complexity:
, where is the number of people and timeis the elapsed time. This is because the solution performs a fixed number of arithmetic operations regardless of the input values. The modulo operation and conditional check are both constant time operations.
Space Complexity:
, as the solution uses only a constant amount of additional memory (the cycle_positionvariable) regardless of the input size. No data structures that grow with input size are used.
Example
Input:
Step-by-Step Walkthrough:
Initialization:
The function
passThePillow1is called withn = 5(number of people) andtime = 21(seconds elapsed).The cycle length is calculated:
(n - 1) * 2 = (5 - 1) * 2 = 8. This represents the time it takes for the pillow to make a complete back-and-forth cycle.
Main Calculation:
The cycle position is calculated using the modulo operation:
cycle_position = time % ((n - 1) * 2) = 21 % 8 = 5This means that after 21 seconds, we are 5 steps into the current cycle.
Decision Point:
The function checks if
cycle_position (5) < n (5).Since 5 is not less than 5, the condition is false.
This indicates that the pillow is moving backward at this point in time.
Result Calculation:
For backward movement, the formula
2 * n - (cycle_position + 1)is used:2 * 5 - (5 + 1) = 10 - 6 = 4This calculation determines the position of the pillow counting from the start of the line when it's moving backward.
Visual Aid: Here's a summary of the calculation:
Step
Description
Value
Input
nNumber of people
5
Input
timeElapsed time
21
Cycle length
(n - 1) * 28
Cycle position
time % cycle_length5
Movement direction
Based on
cycle_position < nBackward
Result
2 * n - (cycle_position + 1)4
Final Result:
The function returns 4, which means after 21 seconds, the pillow is with the fourth person in the line.
July 7 -> 1518. Water Bottles
There are num_bottles water bottles that are initially full of water. You can exchange num_exchange empty water bottles from the market with one full water bottle.
The operation of drinking a full water bottle turns it into an empty bottle.
Given the two integers num_bottles and num_exchange, return the maximum number of water bottles you can drink.
Example 1:
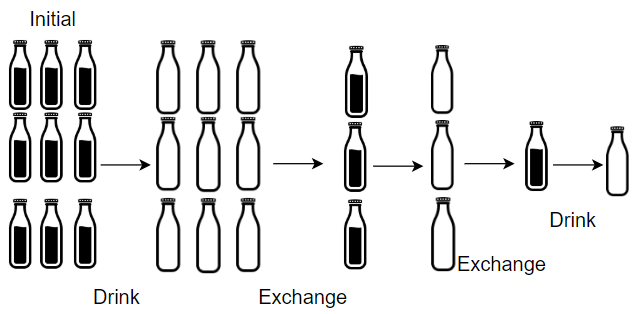
Input: num_bottles = 9, num_exchange = 3
Output: 13
Explanation: You can exchange three empty bottles to get one full water bottle.
Number of water bottles you can drink: 9 + 3 + 1 = 13.
Example 2:

Input: num_bottles = 15, num_exchange = 4
Output: 19
Explanation: You can exchange four empty bottles to get one full water bottle.
Number of water bottles you can drink: 15 + 3 + 1 = 19.
Constraints:
1 <= num_bottles <= 1002 <= num_exchange <= 100
Approach 1: Greedy Simulation
Understanding the Core Idea
The central concept of this solution is to leverage a greedy simulation approach to maximize the number of water bottles drunk. The solution iteratively drinks all available full bottles and exchanges empty bottles for new full ones until no more exchanges are possible.
Greedy Strategy: The algorithm always drinks all available full bottles and exchanges as many empty bottles as possible in each iteration.
Simulation: The process of drinking and exchanging is simulated step by step until the termination condition is met.
Code Walkthrough
Initialization:
total_drinks = num_bottles empty_bottles = num_bottlesWe initialize
total_drinksandempty_bottleswithnum_bottles. This represents drinking all initially available full bottles, which becomes our starting point for total drinks and empty bottles.Exchange Loop:
while empty_bottles >= num_exchange:This loop continues as long as we have enough empty bottles to make an exchange. It's the core of our simulation.
Bottle Exchange Calculation:
exchanged_bottles, unused_bottles = divmod(empty_bottles, num_exchange)Here, we use
divmod()to efficiently calculate two values:exchanged_bottles: The number of full bottles we get by exchanging empty ones.unused_bottles: The number of empty bottles left that couldn't be exchanged.
Updating Total Drinks:
total_drinks += exchanged_bottlesWe increment
total_drinksbyexchanged_bottles, as these new full bottles will be immediately consumed.Updating Empty Bottles:
empty_bottles = exchanged_bottles + unused_bottlesWe update
empty_bottlesfor the next iteration. It includes the bottles we just drank (exchanged_bottles) and the leftover empty bottles from the previous round (unused_bottles).Result Return:
return total_drinksOnce we can no longer exchange bottles, we return the total number of bottles drunk.
Complexity Analysis
Time Complexity:
, where is num_bottlesandis num_exchange. This is because in each iteration, the number of empty bottles is effectively divided bynum_exchange. The number of iterations is logarithmic in the initial number of bottles.
Space Complexity:
, as the algorithm uses only a constant amount of extra space regardless of the input size. It maintains only a few variables ( total_drinks,empty_bottles,exchanged_bottles,unused_bottles) throughout its execution.
Example
Input:
Step-by-Step Walkthrough:
Initialization:
The function starts with
num_bottles = 15andnum_exchange = 4.We initialize
total_drinks = 15(all initial bottles are drunk).We set
empty_bottles = 15(all initial bottles become empty after drinking).
Main Loop (Exchanging empty bottles for full ones):
Iteration 1:
We check if
empty_bottles (15) >= num_exchange (4), which is true.We calculate
divmod(15, 4), which returns(3, 3):exchanged_bottles = 3(we can exchange 3 sets of 4 empty bottles)unused_bottles = 3(3 empty bottles remain after exchanges)
We update
total_drinks:total_drinks = 15 + 3 = 18(add newly acquired full bottles)
We update
empty_bottles:empty_bottles = 3 + 3 = 6(new empties plus unused empties)
Iteration 2:
We check if
empty_bottles (6) >= num_exchange (4), which is true.We calculate
divmod(6, 4), which returns(1, 2):exchanged_bottles = 1(we can exchange 1 set of 4 empty bottles)unused_bottles = 2(2 empty bottles remain after exchanges)
We update
total_drinks:total_drinks = 18 + 1 = 19(add newly acquired full bottle)
We update
empty_bottles:empty_bottles = 1 + 2 = 3(new empty plus unused empties)
Loop Termination:
After the second iteration,
empty_bottles (3) < num_exchange (4).This condition fails the while loop check, so the loop terminates.
At this point, we have drunk all possible bottles and can't exchange anymore.
Visual Aid:
Iteration
Starting Empty Bottles
Exchanged Bottles
Unused Bottles
Total Drinks
Ending Empty Bottles
1
15
3
3
18
6
2
6
1
2
19
3
Result Calculation/Final Steps:
The final result is the value of
total_drinks, which is 19.This represents:
15 initial bottles
3 bottles from the first exchange
1 bottle from the second exchange
The function returns this value (19) as the maximum number of water bottles that can be drunk.
Approach 2: Mathematical Formula
Understanding the Core Idea
The central concept of this solution is to leverage a mathematical formula to directly calculate the maximum number of water bottles that can be drunk. Instead of simulating the process, this approach uses the relationship between the initial number of bottles, the exchange rate, and the maximum possible exchanges to compute the result in a single step.
Mathematical Insight: The solution recognizes that the total number of bottles drunk is the sum of the initial bottles and the additional bottles gained through exchanges.
Direct Calculation: By deriving a formula that captures the exchange process, we can avoid iterative simulation and compute the result instantly.
Code Walkthrough
Formula Application:
return num_bottles + (num_bottles - 1) // (num_exchange - 1)This single line of code encapsulates the entire solution. Let's break it down:
num_bottles: This represents the initial number of full bottles, which are all drunk.(num_bottles - 1) // (num_exchange - 1): This calculates the additional bottles obtained through exchanges.
Understanding the Formula:
num_bottles - 1: This represents the number of empty bottles after drinking the initial bottles, minus one. We subtract one because in the last exchange, we might not have enough empties for a full exchange.num_exchange - 1: This represents the net cost of each exchange in terms of empty bottles. Each exchange gives us 1 full bottle but costsnum_exchangeempty ones, so the net cost isnum_exchange - 1.The integer division
//gives us the maximum number of complete exchanges possible.
Result Calculation: The function returns the sum of the initial bottles and the additional bottles from exchanges, giving us the total number of bottles that can be drunk.
Complexity Analysis
Time Complexity:
, because the function performs a fixed number of arithmetic operations regardless of the input values. It doesn't use any loops or recursive calls, making it constant time.
Space Complexity:
, as the function uses only a constant amount of extra space. It doesn't create any data structures or variables that grow with the input size. All calculations are done in-place with the input parameters.
Example
Input:
Step-by-Step Walkthrough:
Initialization:
The function starts with
num_bottles = 15andnum_exchange = 4.
Main Calculation Steps:
Step 1: Calculate initial empty bottles
We calculate
initial_empty = num_bottles - 1This gives us
initial_empty = 15 - 1 = 14We subtract 1 because in the last exchange, we might not have enough empties for a full exchange
Step 2: Calculate net cost of exchange
We calculate
net_exchange_cost = num_exchange - 1This gives us
net_exchange_cost = 4 - 1 = 3We subtract 1 because each exchange gives us 1 full bottle but costs
num_exchangeempty ones, so the net cost isnum_exchange - 1
Step 3: Calculate additional bottles from exchanges
We calculate
additional_bottles = initial_empty // net_exchange_costThis gives us
additional_bottles = 14 // 3 = 4The integer division
//gives us the maximum number of complete exchanges possible
Step 4: Calculate total bottles drunk
We calculate
total_bottles = num_bottles + additional_bottlesThis gives us
total_bottles = 15 + 4 = 19This sum represents the initial bottles plus all bottles obtained through exchanges
Visual Aid:
Item
Value
Initial Bottles
15
Exchange Rate
4
Initial Empty Bottles
14
Net Exchange Cost
3
Additional Bottles
4
Total Bottles Drunk
19
Result Calculation/Final Steps:
The final result is the value of
total_bottles, which is 19.This represents:
15 initial bottles
4 additional bottles from exchanges
The function returns this value (19) as the maximum number of water bottles that can be drunk.
Mathematical Insight:
This method uses a direct formula to calculate the result, avoiding the need for iteration.
The formula
num_bottles + (num_bottles - 1) // (num_exchange - 1)captures the entire exchange process in one calculation.It's equivalent to our step-by-step calculation but more concise and efficient.