July 2024, Week 2: July 8th - July 14th
July 8 -> 1823. Find the Winner of the Circular Game
There are n friends that are playing a game. The friends are sitting in a circle and are numbered from 1 to n in clockwise order. More formally, moving clockwise from the ith friend brings you to the (i+1)th friend for 1 <= i < n, and moving clockwise from the nth friend brings you to the 1st friend.
The rules of the game are as follows:
Start at the
1stfriend.Count the next
kfriends in the clockwise direction including the friend you started at. The counting wraps around the circle and may count some friends more than once.The last friend you counted leaves the circle and loses the game.
If there is still more than one friend in the circle, go back to step
2starting from the friend immediately clockwise of the friend who just lost and repeat.Else, the last friend in the circle wins the game.
Given the number of friends, n, and an integer k, return the winner of the game.
Example 1:

Input: n = 5, k = 2
Output: 3
Explanation: Here are the steps of the game:
Start at friend 1.
Count two friends clockwise, which are friends 1 and 2.
Friend 2 leaves the circle. Next start is friend 3.
Count two friends clockwise, which are friends 3 and 4.
Friend 4 leaves the circle. Next start is friend 5.
Count two friends clockwise, which are friends 5 and 1.
Friend 1 leaves the circle. Next start is friend 3.
Count two friends clockwise, which are friends 3 and 5.
Friend 5 leaves the circle. Only friend 3 is left, so they are the winner.
Example 2:
Input: n = 6, k = 5
Output: 1
Explanation: The friends leave in this order: 5, 4, 6, 2, 3. The winner is friend 1.
Constraints:
1 <= k <= n <= 500
Approach 1: Simulation with Deque
Understanding the Core Idea
The central concept of this solution is to leverage a deque (double-ended queue) to simulate the circular elimination game efficiently. This approach directly models the game's mechanics by rotating players and removing them as per the rules.
Circular Nature Simulation: The deque allows for efficient rotation of players, mimicking the circular arrangement described in the problem.
Player Elimination: By using the deque's
popleft()method, we can easily remove players from the game when they are counted out.Efficient Rotation: The deque's ability to perform
operations at both ends makes it ideal for simulating the counting process without the need for complex index calculations.
Code Walkthrough
Initialization:
active_players = deque(range(n))We create a deque containing integers from 0 to
n-1, representing the players. Using 0-based indexing simplifies the simulation process.Game Simulation Loop:
while len(active_players) > 1:This loop continues until only one player remains, simulating the entire game process.
Player Rotation:
for _ in range(k - 1): active_players.append(active_players.popleft())We rotate
k-1players from the front to the back of the deque. This simulates the counting process without actually removing any players yet. We usek-1because thekth player will be removed in the next step.Player Elimination:
active_players.popleft()After the rotation, the player at the front of the deque is the
kth player in the count. We remove this player usingpopleft(), simulating their elimination from the game.Result Calculation/Return:
return active_players[0] + 1Once the loop ends, only one player remains in the deque. We return this player's number, adding 1 to convert from 0-based to 1-based indexing as required by the problem statement.
Complexity Analysis
Time Complexity:
, where is the number of players and is the counting interval. This is because we perform eliminations (as we start with players and end with 1), and for each elimination, we rotate the deque times.
Space Complexity:
, where is the number of players. This is because we store all players in the deque initially. The space used remains constant throughout the execution of the algorithm, even as players are eliminated.
Example
Input:
Step-by-Step Walkthrough:
Initialization:
Create a
dequecalledactive_playerswith values[0, 1, 2, 3, 4, 5], representing the players in 0-indexed form.
Main Loop (Elimination Process):
Iteration 1:
Current active players:
[0, 1, 2, 3, 4, 5]We need to remove the fifth player (k=5)
Rotate the deque 4 times (k-1):
Move 0 to the end:
[1, 2, 3, 4, 5, 0]Move 1 to the end:
[2, 3, 4, 5, 0, 1]Move 2 to the end:
[3, 4, 5, 0, 1, 2]Move 3 to the end:
[4, 5, 0, 1, 2, 3]
Remove the front player (4)
Resulting deque:
[5, 0, 1, 2, 3]
Iteration 2:
Current active players:
[5, 0, 1, 2, 3]Rotate 4 times:
Final state after rotation:
[3, 5, 0, 1, 2]
Remove the front player (3)
Resulting deque:
[5, 0, 1, 2]
Iteration 3:
Current active players:
[5, 0, 1, 2]Rotate 4 times:
Final state after rotation:
[5, 0, 1, 2]
Remove the front player (5)
Resulting deque:
[0, 1, 2]
Iteration 4:
Current active players:
[0, 1, 2]Rotate 4 times:
Final state after rotation:
[1, 2, 0]
Remove the front player (1)
Resulting deque:
[2, 0]
Iteration 5:
Current active players:
[2, 0]Rotate 4 times:
Final state after rotation:
[2, 0]
Remove the front player (2)
Resulting deque:
[0]
Loop Termination:
The loop terminates when only one player remains in the
active_playersdeque.Final state of
active_players:[0]
Visual Aids:
The following image represents the simulation process for the example input
n = 6, k = 5where the red elements represent the players that will be removed in each round. The visualization shows the rotation of the deque and the elimination of players until only one player remains.
Iteration Summary:
Round
Active Players
Removed Player
1
[5, 0, 1, 2, 3]
4
2
[5, 0, 1, 2]
3
3
[0, 1, 2]
5
4
[2, 0]
1
5
[0]
2
Result Calculation/Final Steps:
The last remaining player in
active_playersis 0 (0-indexed).Convert to 1-indexed by adding 1: 0 + 1 = 1
Return 1 as the final result.
The winner of the game is player 1 (in 1-indexed form).
Approach 2: Recursive Josephus Problem Solution
Understanding the Core Idea
The central concept of this solution is to leverage the recursive nature of the Josephus problem to calculate the winner's position efficiently. Instead of simulating the game step-by-step, it uses a mathematical relationship between the survivor's position in games with
Recursive Formulation: The solution is built on the idea that the survivor's position in a game with
players can be derived from the survivor's position in a game with players. Position Transformation: The key mathematical relationship used is
(survivor_position + k) % n, which adjusts the survivor's position from an ()-player game to an -player game. Bottom-up Calculation: The solution starts from the base case of one player and builds up to
players through recursive calls.
Code Walkthrough
Helper Function Definition:
def simulate_game(players: int, step: int) -> int:This inner function is defined to handle the recursive calculations. It takes the current number of players and the step size as parameters.
Base Case:
if players == 1: return 0When only one player remains, they are at position 0 (0-based indexing). This serves as the stopping condition for the recursion.
Recursive Case:
survivor_position = simulate_game(players - 1, step)We recursively calculate the survivor's position for a game with one less player. This builds the solution from the bottom up.
Position Adjustment:
return (survivor_position + step) % playersWe adjust the survivor's position from the (n-1)-player game to the n-player game. Adding
stepmoves the position forward, and the modulo operation wraps it around the circle if necessary.Main Function Call and Result Conversion:
return simulate_game(n, k) + 1We call the helper function with the initial number of players and step size. The result is then converted to 1-based indexing by adding 1.
Complexity Analysis
Time Complexity:
, where is the number of players. This is because the function makes exactly recursive calls, each performing constant time operations (addition and modulo). Despite being recursive, the linear nature of the recursion leads to a linear time complexity.
Space Complexity:
, where is the number of players. This space complexity is due to the recursion stack. In the worst case, the recursion will go levels deep before reaching the base case, resulting in stack frames being stored simultaneously.
Example
Input:
Step-by-Step Walkthrough:
Initialization:
The function
findTheWinner2(n=6, k=5)is called.It immediately calls the helper function
simulate_game(6, 5).
Main Recursive Process:
Recursive Call: simulate_game(6, 5)
Not a base case, so it makes a recursive call to
simulate_game(5, 5)
Recursive Call: simulate_game(5, 5)
Not a base case, so it makes a recursive call to
simulate_game(4, 5)
Recursive Call: simulate_game(4, 5)
Not a base case, so it makes a recursive call to
simulate_game(3, 5)
Recursive Call: simulate_game(3, 5)
Not a base case, so it makes a recursive call to
simulate_game(2, 5)
Recursive Call: simulate_game(2, 5)
Not a base case, so it makes a recursive call to
simulate_game(1, 5)
Recursive Call: simulate_game(1, 5)
Base case reached: only one player remains
Returns position 0
Unwinding the Recursion:
simulate_game(2, 5):
Calculates new position: (0 + 5) % 2 = 1
Returns 1
simulate_game(3, 5):
Calculates new position: (1 + 5) % 3 = 0
Returns 0
simulate_game(4, 5):
Calculates new position: (0 + 5) % 4 = 1
Returns 1
simulate_game(5, 5):
Calculates new position: (1 + 5) % 5 = 1
Returns 1
simulate_game(6, 5):
Calculates new position: (1 + 5) % 6 = 0
Returns 0
Visual Aids:
The following image represents the recursive process for the example input
n = 6, k = 5. Each row represents a recursive call, with the top row being the base case. The green elements represent the survivor's position at each step, and the arrows show how the position is calculated and passed up through the recursive calls.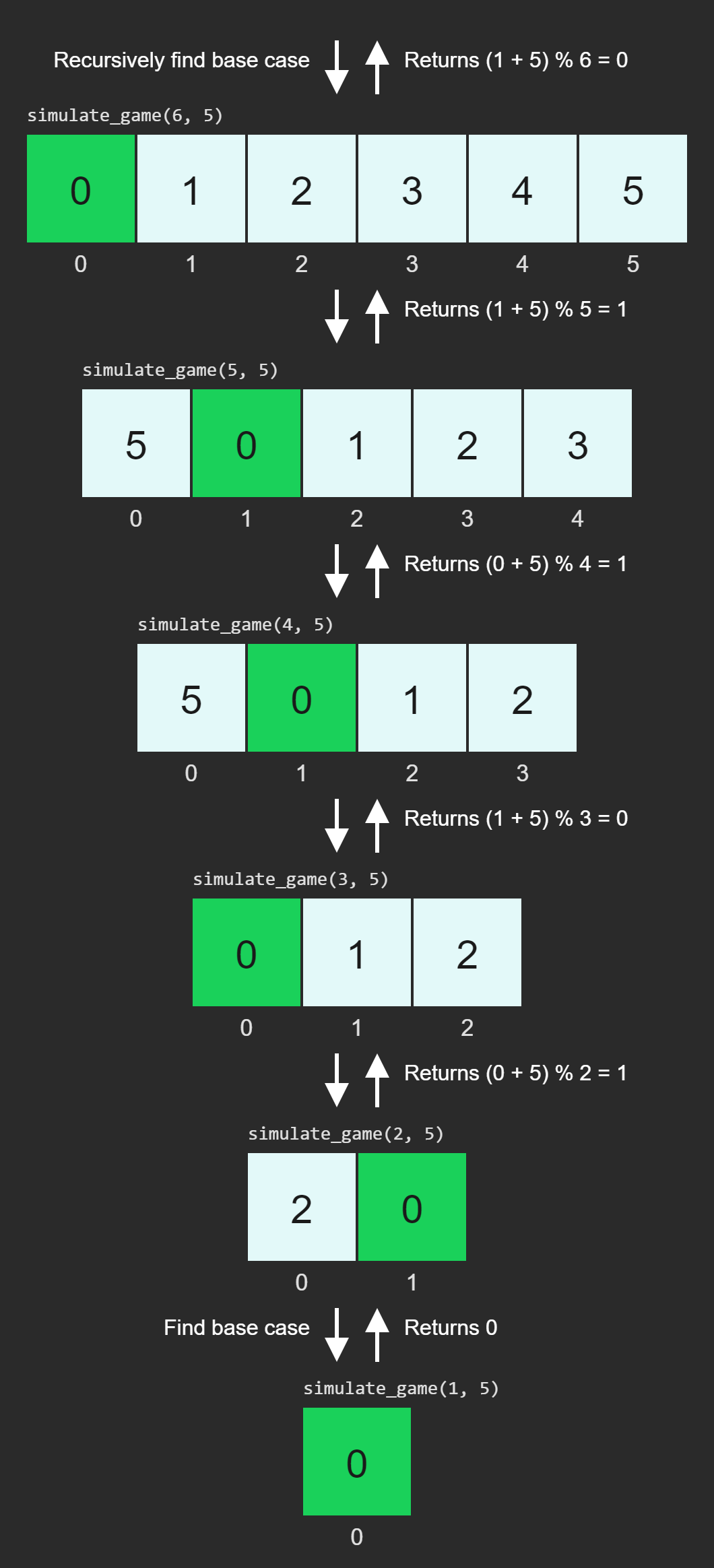
Recursive Calls Summary:
Players
Step
Case
Survivor Position
6
5
Recursive case
0
5
5
Recursive case
1
4
5
Recursive case
1
3
5
Recursive case
0
2
5
Recursive case
1
1
5
Base case
0
Result Calculation/Final Steps:
The recursive function returns 0 (0-indexed result).
The main function adds 1 to convert to 1-indexed: 0 + 1 = 1
Return 1 as the final result.
The winner of the game is player 1 (in 1-indexed form).
Approach 3: Iterative Josephus Problem Solution
Understanding the Core Idea
The central concept of this solution is to solve the Josephus problem iteratively, building up the solution from smaller game sizes to the target size. It leverages the mathematical relationship between survivor positions in games of consecutive sizes.
Iterative Build-up: The solution starts with a trivial game of one player and iteratively calculates the survivor's position for games of increasing sizes up to n players.
Position Transformation: Similar to the recursive approach, it uses the formula
(survivor_position + k) % circle_sizeto adjust the survivor's position as the game size increases.In-place Calculation: Unlike the simulation approach, this method doesn't maintain a list of players, instead working directly with the survivor's position.
Code Walkthrough
Initialization:
survivor_position = 0We start with a survivor position of 0, which represents the winner's position in a trivial 1-player game.
Iterative Calculation Loop:
for circle_size in range(2, n + 1):This loop iterates from 2 to
, calculating the survivor's position for each game size. We start from 2 because the 1-player case is trivially handled by the initialization. Position Adjustment:
survivor_position = (survivor_position + k) % circle_sizeFor each circle size, we adjust the survivor's position from the previous game size. Adding
simulates the counting process, and the modulo operation wraps the position around the current circle size if necessary. Result Conversion and Return:
return survivor_position + 1After the loop completes,
survivor_positionholds the winner's position for the n-player game in 0-based indexing. We add 1 to convert to 1-based indexing as required by the problem statement.
Complexity Analysis
Time Complexity:
, where is the number of players. This is because the function iterates from 2 to , performing a constant number of operations (addition and modulo) in each iteration. Despite solving the problem for all game sizes from 2 to , the linear nature of the iteration results in a linear time complexity.
Space Complexity:
, or constant space. This solution uses only a fixed amount of additional space (the survivor_positionvariable) regardless of the input size. It doesn't use any data structures that grow with the input, nor does it use recursion that would create a variable-sized call stack.
Example
Input:
Step-by-Step Walkthrough:
Initialization:
Set
survivor_position = 0, representing the initial position of the survivor in a hypothetical 1-player game.
Main Loop (Iterative Calculation):
Iteration 1 (circle size 2):
Current state:
survivor_position = 0,circle_size = 2Calculation:
new_position = (0 + 5) % 2 = 1Update
survivor_positionto 1
Iteration 2 (circle size 3):
Current state:
survivor_position = 1,circle_size = 3Calculation:
new_position = (1 + 5) % 3 = 0Update
survivor_positionto 0
Iteration 3 (circle size 4):
Current state:
survivor_position = 0,circle_size = 4Calculation:
new_position = (0 + 5) % 4 = 1Update
survivor_positionto 1
Iteration 4 (circle size 5):
Current state:
survivor_position = 1,circle_size = 5Calculation:
new_position = (1 + 5) % 5 = 1survivor_positionremains 1
Iteration 5 (circle size 6):
Current state:
survivor_position = 1,circle_size = 6Calculation:
new_position = (1 + 5) % 6 = 0Update
survivor_positionto 0
Loop Termination:
The loop terminates when
circle_sizereachesn(6 in this case).Final state of
survivor_position: 0
Visual Aids:
The following image represents the iterative process for the example input
n = 6, k = 5. Each row represents a circle of increasing size, with the green element representing the survivor's position at each step. The arrows and labels show how the position is calculated from one step to the next.
Iteration Summary:
Circle Size
Survivor Position
2
1
3
0
4
1
5
1
6
0
Result Calculation/Final Steps:
The final
survivor_positionis 0 (0-indexed result).Convert to 1-indexed by adding 1: 0 + 1 = 1
Return 1 as the final result.
The winner of the game is player 1 (in 1-indexed form).
July 9 -> 1701. Average Waiting Time
There is a restaurant with a single chef. You are given an array customers, where customers[i] = [arrival_i, time_i]:
arrival_iis the arrival time of theithcustomer. The arrival times are sorted in non-decreasing order.time_iis the time needed to prepare the order of theithcustomer.
When a customer arrives, they give the chef their order, and the chef starts preparing it once they are idle. The customer waits till the chef finishes preparing his order. The chef does not prepare food for more than one customer at a time. The chef prepares food for customers in the order they were given in the input.
Return the average waiting time of all customers. Solutions within 10^(-5) from the actual answer are considered accepted.
Example 1:
Input: customers = [[1,2],[2,5],[4,3]]
Output: 5.00000
Explanation:
The first customer arrives at time 1, the chef takes his order and starts preparing it immediately at time 1, and finishes at time 3, so the waiting time of the first customer is 3 - 1 = 2.
The second customer arrives at time 2, the chef takes his order and starts preparing it at time 3, and finishes at time 8, so the waiting time of the second customer is 8 - 2 = 6.
The third customer arrives at time 4, the chef takes his order and starts preparing it at time 8, and finishes at time 11, so the waiting time of the third customer is 11 - 4 = 7. So the average waiting time = (2 + 6 + 7) / 3 = 5.
Example 2:
Input: customers = [[5,2],[5,4],[10,3],[20,1]]
Output: 3.25000
Explanation:
The first customer arrives at time 5, the chef takes his order and starts preparing it immediately at time 5, and finishes at time 7, so the waiting time of the first customer is 7 - 5 = 2.
The second customer arrives at time 5, the chef takes his order and starts preparing it at time 7, and finishes at time 11, so the waiting time of the second customer is 11 - 5 = 6.
The third customer arrives at time 10, the chef takes his order and starts preparing it at time 11, and finishes at time 14, so the waiting time of the third customer is 14 - 10 = 4.
The fourth customer arrives at time 20, the chef takes his order and starts preparing it immediately at time 20, and finishes at time 21, so the waiting time of the fourth customer is 21 - 20 = 1. So the average waiting time = (2 + 6 + 4 + 1) / 4 = 3.25.
Constraints:
1 <= customers.length <= 10^51 <= arrival_i, time_i <= 10^4arrival_i <= arrival_(i+1)
Approach 1: Linear Simulation
Understanding the Core Idea
The central concept of this solution is to simulate the chef's order processing in real-time, leveraging a linear scan through the customer list to calculate waiting times efficiently. This approach mimics the actual process of a single chef handling orders as they come in.
Time Tracking: The solution maintains a running
order_finish_timeto keep track of when the chef will be available next.Greedy Processing: Orders are processed greedily in the sequence they arrive, without any optimization or reordering.
Cumulative Wait Time: The total waiting time is accumulated as each order is processed, allowing for a simple average calculation at the end.
Code Walkthrough
Initialization:
order_finish_time, total_customer_wait_time = 0, 0The function initializes two key variables:
order_finish_timeto track when the chef will next be available, andtotal_customer_wait_timeto accumulate the total waiting time across all customers.Iterating Through Customers:
for arrival_time, prep_time in customers:This loop processes each customer's order sequentially, unpacking their arrival time and preparation time. This approach aligns with the problem statement that orders are prepared in the given input order.
Calculating Order Finish Time:
order_finish_time = max(arrival_time, order_finish_time) + prep_timeThis line is crucial as it determines when the current order will be finished. It uses
max()to handle two scenarios:If the chef is idle (
order_finish_time<arrival_time), cooking starts atarrival_time.If the chef is busy (
order_finish_time>arrival_time), cooking starts when the previous order finishes. The preparation time is then added to this start time to get the neworder_finish_time.
Calculating and Accumulating Wait Time:
total_customer_wait_time += order_finish_time - arrival_timeThe waiting time for each customer is the difference between when their order is finished and when they arrived. This is added to the running total of wait times.
Calculating Average Wait Time:
average_wait_time = total_customer_wait_time / len(customers) return average_wait_timeAfter processing all customers, the function calculates the average wait time by dividing the total wait time by the number of customers, then returns this value.
Complexity Analysis
Time Complexity:
, where is the number of customers. This is because the function iterates through the customer list exactly once, performing constant-time operations for each customer.
Space Complexity:
, or constant space. This is because the function uses only a fixed amount of additional space ( order_finish_timeandtotal_customer_wait_time) regardless of the input size. It doesn't create any data structures that grow with the input.
Example
Input:
Step-by-Step Walkthrough:
Initialization:
Initialize
order_finish_time = 0(representing when the chef will be available next)Initialize
total_customer_wait_time = 0(to accumulate total waiting time for all customers)
Main Loop (Processing each customer):
Iteration 1 (Customer 1):
Current state:
order_finish_time = 0,total_customer_wait_time = 0Customer arrives at time 5 with order prep time 2
Calculate new
order_finish_time:max(5, 0) + 2 = 7(chef starts at customer's arrival time)
Calculate customer wait time:
7 - 5 = 2Update
total_customer_wait_time:0 + 2 = 2Update
order_finish_timeto 7
Iteration 2 (Customer 2):
Current state:
order_finish_time = 7,total_customer_wait_time = 2Customer arrives at time 5 with order prep time 4
Calculate new
order_finish_time:max(5, 7) + 4 = 11(chef starts after finishing the previous order)
Calculate customer wait time:
11 - 5 = 6Update
total_customer_wait_time:2 + 6 = 8Update
order_finish_timeto 11
Iteration 3 (Customer 3):
Current state:
order_finish_time = 11,total_customer_wait_time = 8Customer arrives at time 10 with order prep time 3
Calculate new
order_finish_time:max(10, 11) + 3 = 14(chef starts after finishing the previous order)
Calculate customer wait time:
14 - 10 = 4Update
total_customer_wait_time:8 + 4 = 12Update
order_finish_timeto 14
Iteration 4 (Customer 4):
Current state:
order_finish_time = 14,total_customer_wait_time = 12Customer arrives at time 20 with order prep time 1
Calculate new
order_finish_time:max(20, 14) + 1 = 21(chef starts at customer's arrival time)
Calculate customer wait time:
21 - 20 = 1Update
total_customer_wait_time:12 + 1 = 13Update
order_finish_timeto 21
Visual Aid:
Customer
Arrival Time
Prep Time
Order Finish Time
Wait Time
Total Wait Time
1
5
2
7
2
2
2
5
4
11
6
8
3
10
3
14
4
12
4
20
1
21
1
13
Result Calculation:
Calculate average waiting time:
total_customer_wait_time / number_of_customers = 13 / 4 = 3.25
The function returns 3.25, which is the average waiting time for all customers.
July 10 -> 1598. Crawler Log Folder
The LeetCode file system keeps a log each time some user performs a change folder operation.
The operations are described below:
"../": Move to the parent folder of the current folder. (If you are already in the main folder, remain in the same folder)."./": Remain in the same folder."x/": Move to the child folder namedx(This folder is guaranteed to always exist).
You are given a list of strings logs where logs[i] is the operation performed by the user at the ith step.
The file system starts in the main folder, then the operations in logs are performed.
Return the minimum number of operations needed to go back to the main folder after the change folder operations.
Example 1:

Input: logs = ["d1/","d2/","../","d21/","./"]
Output: 2
Explanation: Use this change folder operation "../" 2 times and go back to the main folder.
Example 2:
Input: logs = ["d1/","d2/","./","d3/","../","d31/"]
Output: 3
Example 3:
Input: logs = ["d1/","../","../","../"]
Output: 0
Constraints:
1 <= logs.length <= 10^32 <= logs[i].length <= 10logs[i]contains lowercase English letters, digits,'.', and'/'.logs[i]follows the format described in the statement.Folder names consist of lowercase English letters and digits.
Approach 1: Integer Depth Tracking
Understanding the Core Idea
The central concept of this solution is to leverage a single integer variable to represent the current folder depth. This approach simplifies the problem of tracking folder navigation into basic arithmetic operations.
Depth Representation: The main folder is represented by depth 0, and each subfolder increases the depth by 1.
Navigational Operations: Moving into a subfolder increases depth, moving up decreases it, and staying in the same folder doesn't change the depth.
Boundary Handling: The solution prevents going above the main folder by using the
max()function.
Code Walkthrough
Initialization:
folder_depth = 0We initialize
folder_depthto 0, representing the starting position in the main folder. This variable will keep track of our current depth throughout the navigation process.Iterating Through Operations:
for operation in logs:We iterate through each operation in the
logslist. This allows us to process each folder change sequentially, simulating the user's navigation.Handling "Stay in the Same Folder" Operation:
if operation == "./": continueWhen we encounter "./", we simply continue to the next operation without changing
folder_depth. This efficiently handles the "stay in the same folder" operation without unnecessary computations.Handling "Move Up" Operation:
if operation == "../": folder_depth = max(0, folder_depth - 1)For "../", we decrease
folder_depthby 1, but usemax()to ensure it never goes below 0. This elegantly handles moving up from the main folder without requiring an additional conditional check.Handling "Move to Subfolder" Operation:
else: folder_depth += 1For any other operation (which represents moving into a subfolder), we increment
folder_depthby 1. This assumes all other operations are valid "x/" commands as per the problem statement.Result Calculation/Return:
return folder_depthAfter processing all operations,
folder_depthrepresents the current depth from the main folder. This is exactly the number of "../" operations needed to return to the main folder, so we return it directly.
Complexity Analysis
Time Complexity:
, where is the number of operations in the logslist. This is because we iterate through each operation exactly once, performing constant-time operations for each.
Space Complexity:
, as we only use a single integer variable folder_depthregardless of the input size. This solution doesn't require any additional data structures that grow with the input size.
Example
Input:
Step-by-Step Walkthrough:
Initialization:
We start by initializing
folder_depth = 0, representing that we're in the main folder.
Main Loop (Processing each operation):
Iteration 1:
Operation:
'd1/'This is a move to child folder operation.
Action: Increment
folder_depthfrom 0 to 1.We are now one level deep in the folder structure.
Iteration 2:
Operation:
'd2/'Another move to child folder operation.
Action: Increment
folder_depthfrom 1 to 2.We are now two levels deep.
Iteration 3:
Operation:
'./'This operation means stay in the same folder.
Action: No change to
folder_depth, it remains 2.
Iteration 4:
Operation:
'd3/'Another move to child folder operation.
Action: Increment
folder_depthfrom 2 to 3.We are now three levels deep.
Iteration 5:
Operation:
'../'This is a move to parent folder operation.
Action: Decrement
folder_depth, but ensure it doesn't go below 0.Calculation:
max(0, 3 - 1) = 2folder_depthis updated from 3 to 2.
Iteration 6:
Operation:
'd31/'Another move to child folder operation.
Action: Increment
folder_depthfrom 2 to 3.We end up three levels deep again.
Visual Aid:
Operation #
Command
Resulting Depth
1
d1/
1
2
d2/
2
3
./
2
4
d3/
3
5
../
2
6
d31/
3
Result Calculation:
After processing all operations, our final
folder_depthis 3.This means we are three levels deep in the folder structure.
To return to the main folder, we need to perform three
'../'operations.
The function returns 3, which represents the minimum number of '../' operations needed to return to the main folder from our current position.
Approach 2: Stack-Based Folder Tracking
Understanding the Core Idea
The central concept of this solution is to leverage a stack data structure to simulate the folder hierarchy. This approach provides a more intuitive representation of the file system structure.
Stack Representation: Each element in the stack represents a subfolder, with the bottom of the stack being the main folder.
Navigational Operations: Moving into a subfolder pushes it onto the stack, moving up pops the top folder, and staying in the same folder does nothing to the stack.
Depth Calculation: The depth of the current folder is directly represented by the size of the stack.
Code Walkthrough
Initialization:
folder_stack = []We initialize an empty list
folder_stackto represent our folder structure. The empty stack corresponds to being in the main folder.Iterating Through Operations:
for operation in logs:We iterate through each operation in the
logslist, processing them sequentially to simulate the user's navigation.Handling "Stay in the Same Folder" Operation:
if operation == "./": continueWhen we encounter "./", we simply continue to the next operation without modifying the stack. This efficiently handles the "stay in the same folder" operation without unnecessary computations.
Handling "Move Up" Operation:
elif operation == "../": if folder_stack: folder_stack.pop()For "../", we check if the stack is not empty (ensuring we're not in the main folder) and then pop the top element. This simulates moving up one level in the folder hierarchy. The check prevents attempts to move above the main folder.
Handling "Move to Subfolder" Operation:
else: folder_stack.append(operation)For any other operation (which represents moving into a subfolder), we append it to the stack. This simulates entering a new subfolder by adding it to our current path.
Result Calculation/Return:
return len(folder_stack)After processing all operations, the length of
folder_stackrepresents the current depth from the main folder. This is exactly the number of "../" operations needed to return to the main folder, so we return it directly.
Complexity Analysis
Time Complexity:
, where is the number of operations in the logslist. This is because we iterate through each operation exactly once, and each operation (push, pop, or continue) is performed in constant time.
Space Complexity:
in the worst case, where is the number of operations in the logslist. This occurs when all operations are "move to subfolder" operations, causing the stack to grow to the size of the input. In the best case (all operations are "../" or "./"), the space complexity would be.
Example
Step-by-Step Walkthrough:
Initialization:
We start by initializing
folder_stack = [], an empty list representing that we're in the main folder.
Main Loop (Processing each operation):
Iteration 1:
Operation:
'd1/'This is a move to child folder operation.
Action: Append
'd1/'tofolder_stack.Current stack:
['d1/']
Iteration 2:
Operation:
'd2/'Another move to child folder operation.
Action: Append
'd2/'tofolder_stack.Current stack:
['d1/', 'd2/']
Iteration 3:
Operation:
'./'This operation means stay in the same folder.
Action: No change to
folder_stack.Current stack remains:
['d1/', 'd2/']
Iteration 4:
Operation:
'd3/'Another move to child folder operation.
Action: Append
'd3/'tofolder_stack.Current stack:
['d1/', 'd2/', 'd3/']
Iteration 5:
Operation:
'../'This is a move to parent folder operation.
Action: Remove the last item from
folder_stack(pop'd3/').Current stack:
['d1/', 'd2/']
Iteration 6:
Operation:
'd31/'Another move to child folder operation.
Action: Append
'd31/'tofolder_stack.Final stack:
['d1/', 'd2/', 'd31/']
Visual Aid:
The following image illustrates the stack representation after each operation in the example:
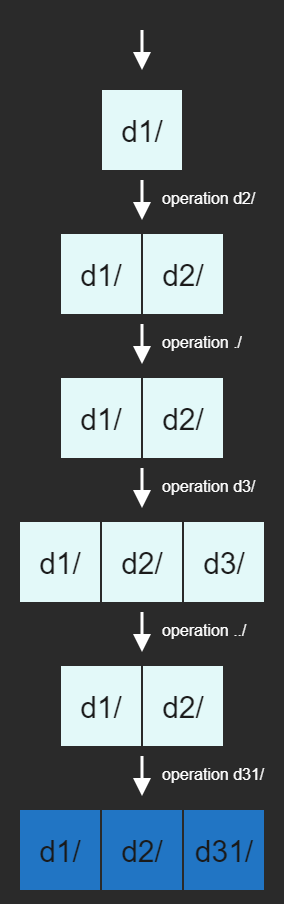
Iteration Summary:
Operation #
Command
Stack Depth
Current Stack
1
d1/
1
['d1/']
2
d2/
2
['d1/', 'd2/']
3
./
2
['d1/', 'd2/']
4
d3/
3
['d1/', 'd2/', 'd3/']
5
../
2
['d1/', 'd2/']
6
d31/
3
['d1/', 'd2/', 'd31/']
Result Calculation:
After processing all operations, our final
folder_stackis['d1/', 'd2/', 'd31/'].The length of this stack is 3.
This means we are three levels deep in the folder structure.
To return to the main folder, we need to perform three
'../'operations, one for each folder in the stack.
The function returns 3, which represents the minimum number of '../' operations needed to return to the main folder from our current position. This is equivalent to the length of the folder_stack at the end of processing all operations.
July 11 -> 1190. Reverse Substrings Between Each Pair of Parentheses
You are given a string s that consists of lower case English letters and brackets.
Reverse the strings in each pair of matching parentheses, starting from the innermost one.
Your result should not contain any brackets.
Example 1:
Input:
s = "(abcd)"Output:
"dcba"
Example 2:
Input:
s = "(u(love)i)"Output:
"iloveu"Explanation: The substring
"love"is reversed first, then the whole string is reversed.
Example 3:
Input:
s = "(ed(et(oc))el)"Output:
"leetcode"Explanation: First, we reverse the substring
"oc", then"etco", and finally, the whole string.
Constraints:
1 <= s.length <= 2000sonly contains lower case English characters and parentheses.It is guaranteed that all parentheses are balanced.
Approach 1: Stack-based Reversal
Understanding the Core Idea
The central concept of this solution is to leverage a stack data structure to handle nested parentheses and perform in-place reversals. This approach allows us to process the string from left to right, reversing substrings within parentheses as we encounter them.
Stack Usage: The stack is used to store characters and handle nested parentheses efficiently.
Immediate Reversal: Substrings within parentheses are reversed as soon as a closing parenthesis is encountered, ensuring proper handling of nested structures.
In-place Processing: The solution modifies the stack contents directly, avoiding the need for additional data structures for each nested level.
Code Walkthrough
Initialization:
stack = []We initialize an empty list
stackto serve as our stack data structure. This stack will store characters from the input string and handle the reversal process.Iterating Through the String:
for char in s:We iterate through each character in the input string
s. This allows us to process the string from left to right, handling each character individually.Handling Closing Parenthesis:
if char == ')': reversed_substring = [] while stack and stack[-1] != '(': reversed_substring.append(stack.pop())When we encounter a closing parenthesis, we start the reversal process. We create a temporary list
reversed_substringto store the characters we'll reverse. We then pop characters from the stack and append them toreversed_substringuntil we find an opening parenthesis. This effectively reverses the order of characters within the parentheses.Removing Opening Parenthesis:
if stack: stack.pop()After extracting the substring to be reversed, we remove the opening parenthesis from the stack. This step ensures that the parentheses themselves are not included in the final result.
Adding Reversed Substring Back to Stack:
stack.extend(reversed_substring)We add the reversed substring back to the stack. This step completes the reversal process for the current pair of parentheses.
Handling Other Characters:
else: stack.append(char)For any character that is not a closing parenthesis (including opening parentheses and regular characters), we simply append it to the stack.
Result Calculation/Return:
return "".join(stack)After processing all characters, the stack contains the final result with all parentheses removed and substrings appropriately reversed. We join the characters in the stack to form the final string and return it.
Complexity Analysis
Time Complexity:
, where is the length of the input string. This is because in the worst case (deeply nested parentheses), we might need to reverse and re-add almost the entire string for each closing parenthesis. For example, in a string like "(((...)))", each closing parenthesis might require reversing almost the entire preceding substring.
Space Complexity:
, where is the length of the input string. This is because in the worst case (no parentheses or all opening parentheses), the stack might need to store all characters of the input string. The reversed_substringlist is temporary and never grows larger than the stack, so it doesn't affect the overall space complexity.
Example
Input:
Step-by-Step Walkthrough:
Initialization:
An empty stack
stack = []is created to store characters and handle parentheses.
Main Loop (Iterating through the input string):
Iteration 1 (
'('):The opening parenthesis is appended to the stack.
Current stack:
['(']
Iterations 2-3 (
'e','l'):Characters
'e'and'l'are appended to the stack.Current stack:
['(', 'e', 'l']
Iterations 4-8 (
'(','a','(','p','m'):These characters, including nested parentheses, are appended to the stack.
Current stack:
['(', 'e', 'l', '(', 'a', '(', 'p', 'm']
Iteration 9 (
')'):Closing parenthesis encountered. The algorithm starts reversing the innermost substring.
'm'and'p'are popped from the stack and stored inreversed_substring.The opening parenthesis
'('is removed.reversed_substring['m', 'p'] is added back to the stack.Current stack:
['(', 'e', 'l', '(', 'a', 'm', 'p']
Iteration 10 (
')'):Another closing parenthesis. The algorithm reverses the next substring.
'p','m', and'a'are popped and stored inreversed_substring.The opening parenthesis
'('is removed.reversed_substring['p', 'm', 'a'] is added back to the stack.Current stack:
['(', 'e', 'l', 'p', 'm', 'a']
Iterations 11-12 (
'x','e'):Characters
'x'and'e'are appended to the stack.Current stack:
['(', 'e', 'l', 'p', 'm', 'a', 'x', 'e']
Iteration 13 (
')'):Final closing parenthesis. The algorithm reverses the entire remaining substring.
All characters except the first
'('are popped and stored inreversed_substring.The opening parenthesis
'('is removed.reversed_substring['e', 'x', 'a', 'm', 'p', 'l', 'e'] becomes the final stack content.
Loop Termination:
The loop terminates after processing all characters in the input string.
Final stack:
['e', 'x', 'a', 'm', 'p', 'l', 'e']
Visual Aid:
Here's a summary of the stack's state after each iteration:
Step
Character
Stack Content
1
(
(2
e
(e3
l
(el4
(
(el(5
a
(el(a6
(
(el(a(7
p
(el(a(p8
m
(el(a(pm9
)
(el(amp10
)
(elpma11
x
(elpmax12
e
(elpmaxe13
)
exampleHere's an image illustrating the stack's state after each iteration, including the reversal process where:
Light blue cells represent characters added to the stack normally.
Red cells indicate opening parentheses that will be removed.
Green cells show characters that are about to be reversed.
Dark blue cells represent reversed substrings that have been added back to the stack.

The visualization demonstrates how the algorithm handles nested parentheses:
It first processes the innermost pair (pm), reversing it to 'mp'.
Then it handles the next level (amp), reversing it to 'pma'.
Finally, it reverses the entire remaining string, resulting in 'example'.
Result Calculation/Final Steps:
The algorithm joins all characters in the final stack to form the result string.
Final Result:
"example"
Approach 2: Two-Pass Traversal with Direction Reversal (Wormhole Teleportation Technique)
Understanding the Core Idea
The central concept of this solution is to leverage a two-pass approach combined with direction reversal to handle nested parentheses efficiently. This method avoids explicit string reversals by cleverly using directional traversal.
Parentheses Pairing: The first pass pairs up matching parentheses, storing their indices for quick access.
Directional Traversal: The second pass builds the result by traversing the string, changing the direction at parentheses to implicitly reverse substrings.
Index Jumping: Instead of pushing and popping from a stack, this approach uses index jumps to navigate between matching parentheses.
Code Walkthrough
Initialization:
parentheses_pairs = {} opening_parentheses = []We initialize an empty dictionary
parentheses_pairsto store the indices of matching parentheses, and a listopening_parenthesesto keep track of opening parentheses indices during the first pass.First Pass - Pairing Parentheses:
for index, char in enumerate(s): if char == '(': opening_parentheses.append(index) elif char == ')': if opening_parentheses: opening_index = opening_parentheses.pop() parentheses_pairs[index] = opening_index parentheses_pairs[opening_index] = indexWe iterate through the string, using a stack-like approach to pair up matching parentheses. When we encounter an opening parenthesis, we add its index to
opening_parentheses. For a closing parenthesis, we pop the last opening parenthesis index and create a two-way mapping inparentheses_pairs. This allows us to quickly jump between matching parentheses in the second pass.Second Pass Initialization:
result = [] current_index = 0 direction = 1 # 1 for forward, -1 for backwardWe initialize an empty list
resultto build our output string,current_indexto keep track of our position in the string, anddirectionto determine whether we're moving forward or backward through the string.Second Pass - Building the Result:
while current_index < len(s): if s[current_index] in '()': current_index = parentheses_pairs[current_index] direction = -direction else: result.append(s[current_index]) current_index += directionWe traverse the string, changing direction when we hit a parenthesis. If the current character is a parenthesis, we jump to its matching pair and reverse direction. Otherwise, we add the character to our result. This clever technique implicitly reverses substrings within parentheses without actually reversing any part of the string.
Result Calculation/Return:
return ''.join(result)After processing all characters, we join the characters in the
resultlist to form the final string and return it.
Complexity Analysis
Time Complexity:
, where is the length of the input string. This is because we make two passes through the string, and in each pass, we process each character exactly once. Even though we change the direction in the second pass, we still visit each character no more than twice in total.
Space Complexity:
, where is the length of the input string. This is because in the worst case (where the string consists entirely of paired parentheses), the parentheses_pairsdictionary would storepairs of indices. The resultlist will also store up tocharacters. The opening_parentheseslist in the first pass could also store up toindices in the worst case, but it's cleared before the second pass begins.
Example
Input:
Step-by-Step Walkthrough:
Initialization:
Two empty data structures are created:
parentheses_pairs = {}: A dictionary to store matching parentheses indices.opening_parentheses = []: A list to keep track of opening parentheses indices.
First Pass: Pairing Parentheses
Iteration 1 ('('):
Opening parenthesis at index 0 is added to
opening_parentheses.Current
opening_parentheses:[0]
Iterations 2-3 ('e', 'l'):
Non-parenthesis characters are skipped.
Iteration 4 ('('):
Opening parenthesis at index 3 is added to
opening_parentheses.Current
opening_parentheses:[0, 3]
Iteration 5 ('a'):
Non-parenthesis character is skipped.
Iteration 6 ('('):
Opening parenthesis at index 5 is added to
opening_parentheses.Current
opening_parentheses:[0, 3, 5]
Iterations 7-8 ('p', 'm'):
Non-parenthesis characters are skipped.
Iteration 9 (')'):
Closing parenthesis found. Paired with the last opening parenthesis.
Popped index 5 from
opening_parentheses.Added pair to
parentheses_pairs:{8: 5, 5: 8}
Iteration 10 (')'):
Another closing parenthesis. Paired with the next opening parenthesis.
Popped index 3 from
opening_parentheses.Updated
parentheses_pairs:{8: 5, 5: 8, 9: 3, 3: 9}
Iterations 11-12 ('x', 'e'):
Non-parenthesis characters are skipped.
Iteration 13 (')'):
Final closing parenthesis. Paired with the first opening parenthesis.
Popped index 0 from
opening_parentheses.Final
parentheses_pairs:{8: 5, 5: 8, 9: 3, 3: 9, 12: 0, 0: 12}
Final Pairing:
Index
Matching Index
8
5
5
8
9
3
3
9
12
0
0
12
Second Pass: Building Result
Initialize
result = [],current_index = 0,direction = 1Step 1:
At index 0 ('('): Jump to matching parenthesis at index 12, reverse direction.
Updated:
result = "", current_index = 11, direction = -1
Steps 2-3:
Process 'e' and 'x' backwards, appending to result.
After step 3:
result = "ex", current_index = 9, direction = -1
Step 4:
At index 9 (')'): Jump to matching parenthesis at index 3, reverse direction.
Updated:
result = "ex", current_index = 4, direction = 1
Step 5:
Process 'a' forward, appending to result.
Updated:
result = "exa", current_index = 5, direction = 1
Step 6:
At index 5 ('('): Jump to matching parenthesis at index 8, reverse direction.
Updated:
result = "exa", current_index = 7, direction = -1
Steps 7-8:
Process 'm' and 'p' backwards, appending to result.
After step 8:
result = "examp", current_index = 5, direction = -1
Steps 9-10:
Navigate through parentheses, changing directions.
After step 10:
result = "examp", current_index = 2, direction = -1
Steps 11-12:
Process 'l' and 'e' backwards, appending to result.
After step 12:
result = "example", current_index = 0, direction = -1
Step 13:
At index 0 ('('): Jump to matching parenthesis at index 12, reverse direction.
Loop terminates as
current_index = 13is out of string bounds.
Visual Aid:
The attached image serves a dual-purpose in explaining the
reverseParentheses2algorithm:First Pass: Parentheses Pairing
The color-coded parentheses demonstrate how the algorithm identifies and pairs matching brackets:
Green cells (indices 0 and 12) represent the outermost pair of parentheses.
Yellow cells (indices 3 and 9) show the second level of nested parentheses.
Blue cells (indices 5 and 8) indicate the innermost pair of parentheses.
This color-coding visualizes the creation of the
parentheses_pairsdictionary, with each color representing a key-value pair.

Second Pass: Result Building
The same image can be used to trace the algorithm's path as it builds the result:
Start at index 0 (green '('): Jump to its pair at index 12, reverse direction to -1.
Moving backwards, append 'e' (index 11) and 'x' (index 10) to the result.
Reach yellow ')' at index 9: Jump to its pair at index 3, reverse direction to +1.
Moving forward, append 'a' (index 4).
Encounter blue '(' at index 5: Jump to its pair at index 8, reverse direction to -1.
Moving backwards, append 'm' (index 7) and 'p' (index 6).
Hit blue '(' at index 5 again: Jump back to index 8, reverse to +1.
Immediately encounter yellow ')' at index 9: Jump to index 3, reverse to -1.
Moving backwards, append 'l' (index 2) and 'e' (index 1).
Reach green '(' at index 0: Jump to index 12, reverse to +1.
Terminate as index 13 is out of bounds.
Result Calculation/Final Steps:
The algorithm has built the result string character by character during the second pass.
Final Result:
"example"
July 12 -> 1717. Maximum Score From Removing Substrings
You are given a string s and two integers x and y. You can perform two types of operations any number of times.
Remove substring
"ab"and gainxpoints.For example, when removing
"ab"from"cabxbae"it becomes"cxbae".
Remove substring
"ba"and gainypoints.For example, when removing
"ba"from"cabxbae"it becomes"cabxe".
Return the maximum points you can gain after applying the above operations on s.
Example 1:
Input:
s = "cdbcbbaaabab", x = 4, y = 5Output: 19
Explanation:
Remove the second
"ba"in"cdbcbbaaabab". Now,s = "cdbcbbaaab"and 5 points are added to the score.Remove
"ab"from"cdbcbbaaab". Now,s = "cdbcbbaa"and 4 points are added to the score.Remove
"ba"from"cdbcbbaa". Now,s = "cdbcba"and 5 points are added to the score.Remove
"ba"from in"cdbcba". Now,s = "cdbc"and 5 points are added to the score. Total score = 5 + 4 + 5 + 5 = 19.
Example 2:
Input:
s = "aabbaaxybbaabb", x = 5, y = 4Output: 20
Constraints:
1 <= s.length <= 10^51 <= x, y <= 10^4sconsists of lowercase English letters.
Approach 1: Stack-Based Greedy Removal
Understanding the Core Idea
The central concept of this solution is to leverage a stack-based approach combined with a greedy strategy to maximize point gain from substring removals. The solution processes the string twice, prioritizing the higher-value substring removal first.
Greedy Prioritization: The algorithm first determines which substring ('ab' or 'ba') yields higher points and processes that substring first. This ensures that the more valuable removals are prioritized.
Stack-based Removal: For each substring type, the function uses a stack to efficiently identify and remove matching substrings in a single pass through the string.
Two-Pass Approach: The string is processed twice, once for each substring type, ensuring all possible removals are made, even if removing one type of substring reveals opportunities for the other type.
Code Walkthrough
Initialization and Prioritization:
high_value_seq, low_value_seq = ('ab', x), ('ba', y) if x < y: high_value_seq, low_value_seq = low_value_seq, high_value_seq total_points = 0The code starts by determining which substring has higher value and sets up tuples to represent these sequences along with their point values. This prioritization is crucial for the greedy approach.
Iterative Processing:
for (first_char, second_char), points in [high_value_seq, low_value_seq]:The function iterates twice, first for the high-value sequence and then for the low-value sequence. This ensures that we always prioritize the more valuable removals while still capturing all possible point gains.
Stack-based Removal:
stack = [] for char in s: if stack and stack[-1] == first_char and char == second_char: stack.pop() total_points += points else: stack.append(char)For each character in the string, the algorithm checks if it forms a target substring with the top of the stack. If so, it removes both characters and adds points. Otherwise, it adds the character to the stack. This efficient approach allows for substring removal in a single pass.
Preparing for the Next Iteration:
s = stackAfter processing one substring type, the remaining characters become the input for the next iteration. This step is crucial as it allows the algorithm to find new opportunities for removal that might have been created by the previous pass.
Result Calculation/Return:
return total_pointsThe function returns the total points accumulated from all substring removals, representing the maximum points that can be gained.
Complexity Analysis
Time Complexity:
, where is the length of the input string. This is because the function processes the string twice in the worst case, once for each substring type. Each character is processed at most twice, resulting in a linear time complexity.
Space Complexity:
, where is the length of the input string. In the worst case, where no removals are possible, the stack would store all characters of the input string. Therefore, the space required grows linearly with the input size.
Example
Input:
Step-by-Step Walkthrough:
Initialization:
The function starts by determining which substring has a higher value:
high_value_seq = ('ba', 5)(since y > x)low_value_seq = ('ab', 4)
total_pointsis initialized to 0
Main Loop (Processing high-value sequence
'ba'):Iteration 1-6:
Characters
'c','d','b','c','b','b'are pushed onto the stack.Stack after six iterations: ['c', 'd', 'b', 'c', 'b', 'b']
Iteration 7:
Current character:
'a'Forms
'ba'with top of stackPop
'b'from stack, add 5 pointstotal_points = 5Stack: ['c', 'd', 'b', 'c', 'b']
Iteration 8:
Current character:
'a'Forms another
'ba'with top of stackPop
'b'from stack, add 5 pointstotal_points = 10Stack: ['c', 'd', 'b', 'c']
Iteration 9-10:
Push
'a'and'b'onto stackStack: ['c', 'd', 'b', 'c', 'a', 'b']
Iteration 11:
Current character:
'a'Forms
'ba'with top of stackPop
'b'from stack, add 5 pointstotal_points = 15Stack: ['c', 'd', 'b', 'c', 'a']
Iteration 12:
Push
'b'onto stackFinal stack after the high-value sequence: ['c', 'd', 'b', 'c', 'a', 'b']
Second Loop (Processing low-value sequence
'ab'):The remaining string
'cdbcab'is processed for'ab'sequencesIterations 1-5:
Characters
'c','d','b','c','a'are pushed onto the new stack
Iteration 6:
Current character: 'b'
Forms 'ab' with top of stack
Pop 'a' from stack, add 4 points
total_points = 19Final stack: ['c', 'd', 'b', 'c']
Visual Aid:
These images illustrate the stack's state during each iteration of the maximumGain1 function, showing how it processes the input string
"cdbcbbaaabab":Dark blue cells represent characters newly pushed onto the stack.
Light blue cells show characters already on the stack from previous iterations.
Red cells indicate characters that form a high-value 'ba' or low-value 'ab' pair and will be removed.
The total points accumulated are shown for each iteration.
The visualization demonstrates how the function prioritizes removing 'ba' pairs first, then processes the remaining string for 'ab' pairs.
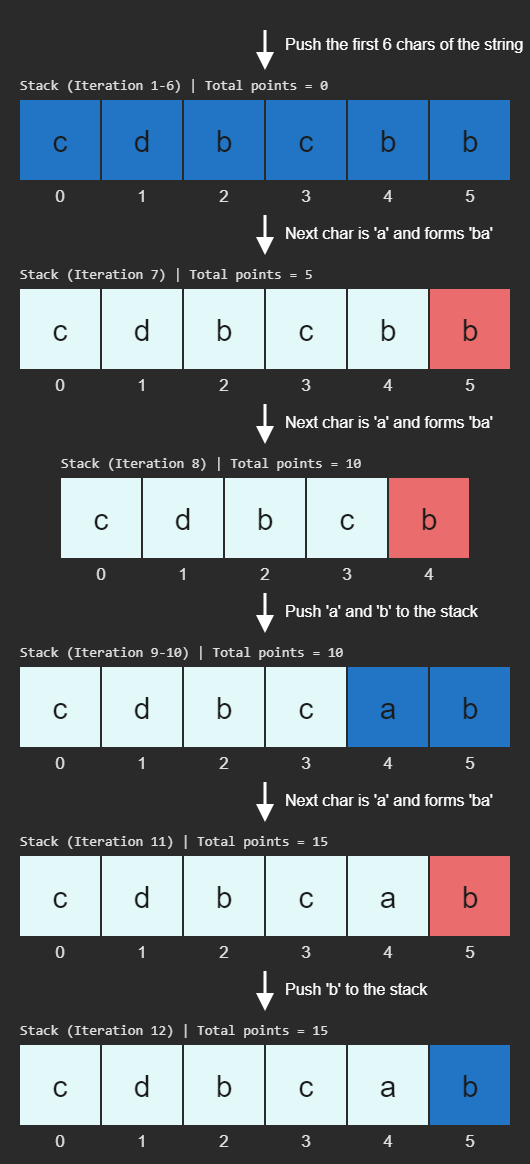
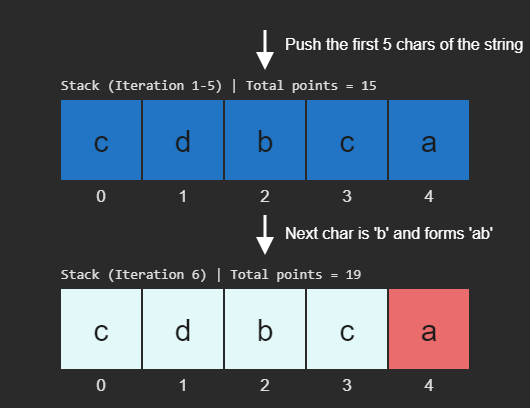
Here's a summary of the stack changes and point accumulation for each substring type: High-Value Sequence
'ba':Iteration
Current Char
Stack After
Points Added
Total Points
1-6
c,d,b,c,b,b
cdbcbb0
0
7
a
cdbcb5
5
8
a
cdbc5
10
9-10
a,b
cdbcab0
10
11
a
cdbca5
15
12
b
cdbcab0
15
Low-Value Sequence
'ab':Iteration
Current Char
Stack After
Points Added
Total Points
1-5
c,d,b,c,a
cdbca0
15
6
b
cdbc4
19
Result Calculation/Final Steps:
After processing both high-value and low-value sequences, the final
total_pointsis 19.This represents the maximum points that can be gained by removing
'ba'and'ab'substrings from the input string.
Approach 2: Single-Pass Greedy Counting
Understanding the Core Idea
The central concept of this solution is to use a single-pass, greedy approach with character counting to maximize point gain from substring removals. This method processes the string once, making immediate decisions about high-value pairs while deferring low-value pair decisions.
Greedy Prioritization: The algorithm prioritizes removing the higher-value substring whenever possible, ensuring optimal point accumulation.
Character Counting: Instead of using a stack, this approach keeps track of unpaired characters, allowing for efficient pair identification and removal.
Deferred Processing: Low-value pair removals are deferred until necessary, ensuring that no high-value pair opportunities are missed.
Code Walkthrough
Initialization and Prioritization:
high_value_char, low_value_char = 'a', 'b' if x < y: x, y = y, x high_value_char, low_value_char = low_value_char, high_value_char total_points = 0 unpaired_high_count, unpaired_low_count = 0, 0The code determines which character pair has a higher value and sets up variables to track points and unpaired character counts. This setup is crucial for the greedy approach and efficient counting.
Single-Pass Processing:
for char in s:The function processes the string in a single pass, making decisions for each character as it's encountered. This is a key efficiency improvement over the two-pass approach.
High-Value Character Handling:
if char == high_value_char: unpaired_high_count += 1 elif char == low_value_char: if unpaired_high_count > 0: unpaired_high_count -= 1 total_points += x else: unpaired_low_count += 1When a high-value character is encountered, it's counted. For a low-value character, the algorithm immediately pairs it with a high-value character if available, adding points. Otherwise, it's counted as unpaired.
Resetting Counts on Non-Pair Characters:
elif unpaired_high_count: if unpaired_low_count: total_points += min(unpaired_high_count, unpaired_low_count) * y unpaired_high_count, unpaired_low_count = 0, 0 else: unpaired_high_count = 0 elif unpaired_low_count: unpaired_low_count = 0When a character that's not part of any pair is encountered, the algorithm processes any accumulated low-value pairs and resets counts. This ensures that pairs are only formed within continuous sequences of relevant characters.
Final Processing:
if unpaired_high_count and unpaired_low_count: total_points += min(unpaired_high_count, unpaired_low_count) * y return total_pointsAfter processing all characters, any remaining low-value pairs are accounted for, and the total points are returned.
Complexity Analysis
, where is the length of the input string. This is because the function processes each character in the string exactly once in a single pass. Each operation within the loop (counting, point calculation) is constant time, resulting in linear overall time complexity.
Space Complexity:
, as the algorithm uses only a constant amount of extra space regardless of the input size. It maintains a fixed number of variables (counters and point totals) that do not grow with the input size.
Example
Input:
Step-by-Step Walkthrough:
Initialization:
Since
y > x, we swap the high and low value characters:high_value_char = 'b', withpoints = 5low_value_char = 'a', withpoints = 4
total_points,unpaired_high_count, andunpaired_low_countare all initialized to 0
Main Loop (Processing characters one by one):
Iterations 1-2:
Characters 'c' and 'd' are non-pair characters.
No action is taken, counts remain unchanged.
Iteration 3:
Current character: 'b' (high-value char)
Increment
unpaired_high_countto 1total_pointsremains 0
Iteration 4:
Current character: 'c' (non-pair char)
Reset
unpaired_high_countto 0 as no matching low-value char was foundtotal_pointsremains 0
Iterations 5-6:
Current characters: 'b', 'b' (high-value chars)
Increment
unpaired_high_countto 2total_pointsremains 0
Iteration 7:
Current character: 'a' (low-value char)
Form a high-value pair 'ba'
Decrement
unpaired_high_countto 1Add 5 points,
total_points = 5
Iteration 8:
Current character: 'a' (low-value char)
Form another high-value pair 'ba'
Decrement
unpaired_high_countto 0Add 5 points,
total_points = 10
Iteration 9:
Current character: 'a' (low-value char)
No matching high-value char, increment
unpaired_low_countto 1total_pointsremains 10
Iteration 10:
Current character: 'b' (high-value char)
Increment
unpaired_high_countto 1total_pointsremains 10
Iteration 11:
Current character: 'a' (low-value char)
Form a high-value pair 'ba'
Decrement
unpaired_high_countto 0Add 5 points,
total_points = 15
Iteration 12:
Current character: 'b' (high-value char)
Increment
unpaired_high_countto 1unpaired_low_countremains 1total_pointsremains 15
Final Check for Remaining Pairs:
Both
unpaired_high_countandunpaired_low_countare 1Form a low-value pair 'ab'
Add 4 points,
total_points = 19
Visual Aid:
Here's a summary of the character processing and point accumulation:
Iteration
Current Char
Unpaired High Count
Unpaired Low Count
Total Points
1
c
0
0
0
2
d
0
0
0
3
b
1
0
0
4
c
0
0
0
5
b
1
0
0
6
b
2
0
0
7
a
1
0
5
8
a
0
0
10
9
a
0
1
10
10
b
1
1
10
11
a
0
1
15
12
b
1
1
15
Final
N/A
1
1
19
Result Calculation/Final Steps:
After processing all characters and checking for remaining pairs, the final
total_pointsis 19.This represents the maximum points that can be gained by removing 'ba' and 'ab' substrings from the input string.
July 13 -> 2751. Robot Collisions
There are n 1-indexed robots, each having a position on a line, health, and movement direction.
You are given 0-indexed integer arrays positions, healths, and a string directions (directions[i] is either 'L' for left or 'R' for right). All integers in positions are unique.
All robots start moving on the line simultaneously at the same speed in their given directions. If two robots ever share the same position while moving, they will collide.
If two robots collide, the robot with lower health is removed from the line, and the health of the other robot decreases by one. The surviving robot continues in the same direction it was going. If both robots have the same health, they are both removed from the line.
Your task is to determine the health of the robots that survive the collisions, in the same order that the robots were given, i.e., final heath of robot 1 (if survived), final health of robot 2 (if survived), and so on. If there are no survivors, return an empty array.
Return an array containing the health of the remaining robots (in the order they were given in the input), after no further collisions can occur.
Note: The positions may be unsorted.
Example 1:
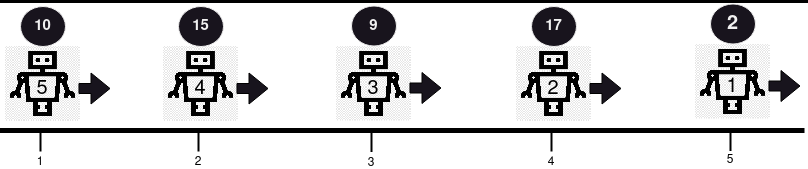
Input:
positions = [5,4,3,2,1], healths = [2,17,9,15,10], directions = "RRRRR"Output: [2,17,9,15,10]
Explanation:
No collision occurs in this example, since all robots are moving in the same direction.
So, the health of the robots in order from the first robot is returned, [2, 17, 9, 15, 10].
Example 2:
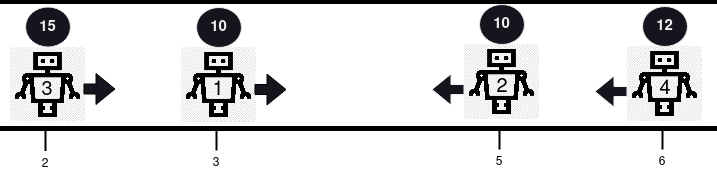
Input:
positions = [3,5,2,6], healths = [10,10,15,12], directions = "RLRL"Output: [14]
Explanation:
There are two collisions in this example.
Firstly, robot 1 and robot 2 will collide, and since both have the same health, they will be removed from the line.
Next, robot 3 and robot 4 will collide, and since robot 4's health is smaller, it gets removed, and robot 3's health becomes 15 - 1 = 14.
Only robot 3 remains, so we return [14].
Example 3:
Input:
positions = [1,2,5,6], healths = [10,10,11,11], directions = "RLRL"Output: []
Explanation:
Robot 1 and robot 2 will collide, and since both have the same health, they are both removed.
Robots 3 and 4 will collide, and since both have the same health, they are both removed.
So, we return an empty array, [].
Constraints:
1 <= positions.length == healths.length == directions.length == n <= 10^51 <= positions[i], healths[i] <= 10^9directions[i] == 'L'ordirections[i] == 'R'All values in
positionsare distinct
Approach 1: Sorted Position-based Simulation with Stack
Understanding the Core Idea
The central concept of this solution is to leverage a sorting-based approach combined with a stack data structure to efficiently simulate robot collisions on a line. This approach allows for handling collisions in the correct order while minimizing unnecessary comparisons.
Sorting by Position: The solution first sorts the robots by their positions, ensuring that collisions are processed in the correct spatial order.
Stack for Right-moving Robots: A stack is used to keep track of right-moving robots, which allows for efficient collision detection with left-moving robots.
Collision Simulation: The algorithm simulates collisions by iterating through the sorted robots and handling collisions between left-moving robots and any right-moving robots they encounter.
Code Walkthrough
Sorting Robot Indices:
sorted_robot_indices = sorted(range(len(positions)), key=lambda x: positions[x])This line creates a list of indices sorted based on the robots' positions. By sorting indices instead of the actual data, we maintain the original order of robots for the final output while still being able to process them in order of position.
Stack Initialization:
right_moving_robot_stack = []This stack will store the indices of right-moving robots. It's used to efficiently handle collisions with left-moving robots.
Collision Simulation Loop:
for current_robot_index in sorted_robot_indices: if directions[current_robot_index] == 'R': right_moving_robot_stack.append(current_robot_index) else: while (right_moving_robot_stack and healths[current_robot_index] > 0): colliding_robot_index = right_moving_robot_stack[-1] handle_collision(colliding_robot_index, current_robot_index)This loop iterates through the sorted robot indices. For right-moving robots, it simply adds them to the stack. For left-moving robots, it checks for collisions with right-moving robots on the stack and handles them using the
handle_collisionfunction. The main idea here is to process collisions in the correct order while avoiding unnecessary comparisons.Collision Handling:
def handle_collision(left_robot_index, right_robot_index): health_diff = healths[left_robot_index] - healths[right_robot_index] if health_diff < 0: healths[left_robot_index] = 0 healths[right_robot_index] -= 1 right_moving_robot_stack.pop() elif health_diff > 0: healths[right_robot_index] = 0 healths[left_robot_index] -= 1 else: healths[left_robot_index], healths[right_robot_index] = 0, 0 right_moving_robot_stack.pop()This function handles the collision between two robots. It compares their health, updates them accordingly, and removes robots from the simulation if their health reaches 0. Here we handle three cases:
The left robot has lower health: Remove the left robot (health set to 0) and decrease the left robot's health by 1 since it survives. Since the left robot is on the stack, it's also removed from the simulation.
The right robot has lower health: Remove the right robot (health set to 0) and decrease the left robot's health by 1. Since the left robot survives, it stays in the stack.
Both robots have the same health: Remove both robots (healths set to 0). Since the left robot is on the stack, it's also removed.
Result Calculation:
surviving_healths = [health for health in healths if health > 0] return surviving_healthsFinally, the function creates a list of surviving robot healths by filtering out robots with zero health, and returns this list.
Complexity Analysis
Time Complexity:
, where is the number of robots. This is because: Sorting the robot indices takes
time. The main loop iterates through all robots once, which is
. Each robot can be involved in at most one collision, so the total number of collision handlings is
. The final filtering of surviving robots is
.
The dominant factor is the initial sorting, hence the overall time complexity is
Space Complexity:
, where is the number of robots. This is because: We store the sorted indices of robots, which takes
space. The stack of right-moving robots can, in the worst case, contain all robots, taking
space. The final list of surviving healths is at most size
.
All other variables use constant space, so the overall space complexity is
Example
Input:
Step-by-Step Walkthrough:
Initialization:
The function starts by printing the input parameters:
positions = [3, 5, 2, 6]healths = [10, 12, 15, 12]directions = "RLRL"
It then initializes key variables:
sorted_robot_indices = [2, 0, 1, 3]: This is the order in which robots will be processed, sorted by their positions.right_moving_robot_stack = []: An empty stack to keep track of robots moving right.
Main Loop (Robot Collision Simulation):
Iteration 1 (Robot 3):
Position: 2, Health: 15, Direction: R
This robot is moving right, so it's added to the
right_moving_robot_stack.Updated
right_moving_robot_stack:[2]
Iteration 2 (Robot 1):
Position: 3, Health: 10, Direction: R
This robot is also moving right, so it's added to the
right_moving_robot_stack.Updated
right_moving_robot_stack:[2, 0]
Iteration 3 (Robot 2):
Position: 5, Health: 12, Direction: L
This robot is moving left, so we check for collisions with right-moving robots.
First collision with Robot 1 (Last right-moving robot):
Robot 1's health (10) is less than Robot 2's health (12).
Robot 1 is destroyed (health becomes 0).
Robot 2's health decreases by 1 to 11.
Robot 1 is removed from the
right_moving_robot_stack.
Second collision with Robot 3 (the only remaining right-moving robot):
Robot 3's health (15) is greater than Robot 2's health (11).
Robot 2 is destroyed (health becomes 0).
Robot 3's health decreases by 1 to 14.
Iteration 4 (Robot 4):
Position: 6, Health: 12, Direction: L
This robot is moving left, so we check for collisions.
It collides with Robot 3 (the last remaining robot in the
right_moving_robot_stack).Collision handling:
Robot 3's health (14) is greater than Robot 4's health (12).
Robot 4 is destroyed (health becomes 0).
Robot 3's health decreases by 1 to 13.
Loop Termination:
The loop terminates after processing all robots in
sorted_robot_indices.Final state of
right_moving_robot_stack:[2](only Robot 3 remains)
Visual Aids: Here's a summary table of the iterations:
Iteration
Robot
Position
Health
Direction
Right-moving Stack
1
3
2
15
R
[2]
2
1
3
10
R
[2, 0]
3
2
5
0
L
[2]
4
4
6
0
L
[2]
Result Calculation/Final Steps:
The function creates a list of surviving robot healths:
It iterates through the
healthslist and includes only non-zero values.
In this case, only Robot 3 survived with health of 13.
The final result is
[13], which is then returned by the function.
July 14 -> 726. Number of Atoms
Given a string formula representing a chemical formula, return the count of each atom.
The atomic element always starts with an uppercase character, then zero or more lowercase letters, representing the name.
One or more digits representing that element's count may follow if the count is greater than 1. If the count is 1, no digits will follow.
For example,
"H2O"and"H2O2"are possible, but"H1O2"is impossible.
Two formulas are concatenated together to produce another formula.
For example,
"H2O2He3Mg4"is also a formula.
A formula placed in parentheses, and a count (optionally added) is also a formula.
For example,
"(H2O2)"and"(H2O2)3"are formulas.
Return the count of all elements as a string in the following form: the first name (in sorted order), followed by its count (if that count is more than 1), followed by the second name (in sorted order), followed by its count (if that count is more than 1), and so on.
The test cases are generated so that all the values in the output fit in a 32-bit integer.
Example 1:
Input:
formula = "H2O"Output:
"H2O"Explanation: The count of elements are
{'H': 2, 'O': 1}.
Example 2:
Input:
formula = "Mg(OH)2"Output:
"H2MgO2"Explanation: The count of elements are
{'H': 2, 'Mg': 1, 'O': 2}.
Example 3:
Input:
formula = "K4(ON(SO3)2)2"Output:
"K4N2O14S4"Explanation: The count of elements are
{'K': 4, 'N': 2, 'O': 14, 'S': 4}.
Constraints:
1 <= formula.length <= 1000formulaconsists of English letters, digits,'(', and')'.formulais always valid.
Approach 1: Stack-based Parsing with Nested Counting
Understanding the Core Idea
The central concept of this solution is to leverage a stack-based approach to handle nested formulas within parentheses, combined with a defaultdict for efficient atom counting. This technique allows for parsing complex chemical formulas with nested structures in a single pass through the input string.
Stack for Nested Formulas: The solution uses a stack of defaultdicts to keep track of atom counts at different nesting levels. This allows for handling nested formulas within parentheses efficiently.
Single-Pass Parsing: The algorithm processes the formula string character by character, handling three main cases: opening parentheses, closing parentheses, and atoms. This approach allows for efficient parsing without the need for multiple passes.
Dynamic Counting: By using a
defaultdict, the solution can dynamically add new atoms and update their counts without explicitly checking for existence first.
Code Walkthrough
Initialization:
formula_length = len(formula) atoms_stack = [defaultdict(int)] index = 0The code initializes the length of the formula, creates a stack with an initial empty
defaultdictfor atom counts, and sets up an index to traverse the formula string.Main Parsing Loop:
while index < formula_length:This loop iterates through each character in the formula string, processing it based on its type.
Handling Opening Parenthesis:
if formula[index] == '(': # Start of a new nested formula atoms_stack.append(defaultdict(int)) index += 1When an opening parenthesis is encountered, a new
defaultdictis added to the stack to start counting atoms in a new nested level.Handling Closing Parenthesis:
elif formula[index] == ')': # End of a nested formula index += 1 start_index = index while index < formula_length and formula[index].isdigit(): index += 1 count_multiplier = int(formula[start_index:index] or 1) # Multiply and merge nested atom counts with parent formula nested_atom_counts = atoms_stack.pop() for atom, count in nested_atom_counts.items(): atoms_stack[-1][atom] += count * count_multiplierWhen a closing parenthesis is encountered, the code extracts any following number as a multiplier for the nested formula. If no number follows, it defaults to 1. The code then pops the nested atom counts from the stack, and adds these counts (multiplied by the multiplier) to the parent level's counts.
Handling Atoms:
elif formula[index].isupper(): # Start of a new atom start_index = index index += 1 while index < formula_length and formula[index].islower(): index += 1 atom_name = formula[start_index:index] # Parse the count for this atom start_index = index while index < formula_length and formula[index].isdigit(): index += 1 count = int(formula[start_index:index] or 1) # Add atom count to current formula level atoms_stack[-1][atom_name] += countWhen an uppercase letter is encountered (indicating the start of an atom), the code extracts the full atom name and its count (If no digits follow, the count defaults to 1). Then, it adds this count to the current level's atom counts.
Result Calculation/Return:
# Format the final result formatted_atom_counts = "".join(atom + (str(count) if count > 1 else "") for atom, count in sorted(atoms_stack[0].items())) return formatted_atom_countsThe final result is calculated by sorting the atoms in the outermost
defaultdict(representing the entire formula) and formatting each atom with its count if greater than 1.
Complexity Analysis
Time Complexity:
, where is the length of the formula string. The main loop iterates through each character once, which is . However, when processing closing parentheses, we may need to update counts for all atoms in the nested formula, which could be up to operations. In the worst case of deeply nested formulas, this could happen times, leading to a quadratic time complexity.
Space Complexity:
, where is the length of the formula string. In the worst case of deeply nested formulas, the stack could grow to size . Each defaultdictin the stack stores at most 26 entries (one for each uppercase letter), so the space complexity remains linear with respect to the input size.
Example
Input:
Step-by-Step Walkthrough:
Initialization:
Set
formula_length = 15(length of the input string)Initialize
atoms_stack = [defaultdict(int)]with one empty dictionary
Main Algorithm Process:
Iteration 1 (index 0):
Character: 'K' (uppercase)
Parse atom name: 'K'
Parse count: '32'
Update
atoms_stack[-1]['K'] = 32:[{K: 32}]
Iteration 2 (index 3):
Character: '(' (opening parenthesis)
Append new
defaultdict(int)toatoms_stack:[{K: 32}, {}]
Iteration 3 (index 4):
Character: 'O' (uppercase)
Parse atom name: 'O'
No explicit count, so use 1
Update
atoms_stack[-1]['O'] = 1:[{K: 32}, {O: 1}]
Iteration 4 (index 5):
Character: 'N' (uppercase)
Parse atom name: 'N'
No explicit count, so use 1
Update
atoms_stack[-1]['N'] = 1:[{K: 32}, {O: 1, N: 1}]
Iteration 5 (index 6):
Character: '(' (opening parenthesis)
Append new
defaultdict(int)toatoms_stack:[{K: 32}, {O: 1, N: 1}, {}]
Iteration 6 (index 7):
Character: 'S' (uppercase)
Parse atom name: 'S'
No explicit count, so use 1
Update
atoms_stack[-1]['S'] = 1:[{K: 32}, {O: 1, N: 1}, {S: 1}]
Iteration 7 (index 8):
Character: 'O' (uppercase)
Parse atom name: 'O'
Parse count: '3'
Update
atoms_stack[-1]['O'] = 3:[{K: 32}, {O: 1, N: 1}, {S: 1, O: 3}]
Iteration 8 (index 10):
Character: ')' (closing parenthesis)
Parse count: '10'
Pop last dictionary from
atoms_stack:{S: 1, O: 3}Multiply counts:
{'S': 1 * 10, 'O': 3 * 10}Add to the previous level:
atoms_stack[-1]['S'] += 10,atoms_stack[-1]['O'] += 30Current state of
atoms_stack:[{'K': 32}, {'O': 31, 'N': 1, 'S': 10}]
Iteration 9 (index 13):
Character: ')' (closing parenthesis)
Parse count: '2'
Pop last dictionary from
atoms_stack:{'O': 31, 'N': 1, 'S': 10}Multiply counts:
{'O': 31 * 2, 'N': 1 * 2, 'S': 10 * 2}Add to previous level:
atoms_stack[-1]['O'] += 62,atoms_stack[-1]['N'] += 2,atoms_stack[-1]['S'] += 20Current state of
atoms_stack:[{'K': 32, 'O': 62, 'N': 2, 'S': 20}]
Loop Termination:
The loop terminates when
indexreachesformula_length(15)Final state of
atoms_stack[0]:{'K': 32, 'O': 62, 'N': 2, 'S': 20}
Visual Aid:
Iteration
Current Char
Action
atoms_stack[-1] After Action
1
'K'
Add K:32
{'K': 32}
2
'('
New dict
{}
3
'O'
Add O:1
{'O': 1}
4
'N'
Add N:1
{'O': 1, 'N': 1}
5
'('
New dict
{}
6
'S'
Add S:1
{'S': 1}
7
'O'
Add O:3
{'S': 1, 'O': 3}
8
')'
Multiply by 10, merge
{'O': 31, 'N': 1, 'S': 10}
9
')'
Multiply by 2, merge
{'K': 32, 'O': 62, 'N': 2, 'S': 20}
Result Calculation/Final Steps:
Sort the atoms alphabetically: K, N, O, S
For each atom, append its name and count (if > 1) to the result string
Final result: "K32N2O62S20"
Approach 2: Two-Pass Parsing with Pre-calculated Multipliers
Understanding the Core Idea
The central concept of this solution is to leverage a two-pass parsing technique to efficiently count atoms in a complex chemical formula. This approach addresses the challenge of nested parentheses and varying multipliers by pre-calculating multipliers for each position in the formula.
Two-Pass Strategy: The solution uses two passes through the formula string - a reverse pass to calculate multipliers, and a forward pass to count atoms.
Multiplier Pre-calculation: By calculating multipliers in the first pass, the solution avoids repeated calculations and simplifies the atom counting process.
Stack for Nested Structures: A stack is used to handle nested parentheses, allowing the solution to correctly apply multipliers at different levels of nesting.
Efficient Atom Counting: The second pass uses the pre-calculated multipliers to count atoms accurately, even in complex nested structures.
Code Walkthrough
Initialization:
formula_length = len(formula) multiplier_stack = [1] multiplier_at_index = [1] * formula_length current_multiplier = 1 current_count_str = ""This section initializes key variables:
formula_length: Stores the length of the input formula for efficient access.multiplier_stack: A stack to handle nested structures, initialized with 1 for the base level.multiplier_at_index: A list to store pre-calculated multipliers for each character position.current_multiplier: Keeps track of the current multiplier value as we parse the formula.current_count_str: A string to accumulate digits when parsing numbers.
First Pass: Multiplier Calculation (Part 1):
# First pass: Calculate multipliers index = formula_length - 1 while index >= 0: current_char = formula[index] if current_char.isdigit(): current_count_str += current_char elif current_char.isalpha(): current_count_str = ""This begins the reverse iteration through the formula:
We start from the end of the string (
formula_length - 1) and move backwards.For digits, we accumulate them in
current_count_str(in reverse order).For letters, we reset
current_count_str, as we've finished parsing a number.
First Pass: Multiplier Calculation (Part 2):
elif current_char == ')': # Start of a nested formula (reading right to left) new_multiplier = int(current_count_str[::-1] or 1) multiplier_stack.append(new_multiplier) current_multiplier *= new_multiplier current_count_str = "" elif current_char == '(': # End of a nested formula (reading right to left) current_multiplier //= multiplier_stack.pop()This section handles parentheses:
For a closing parenthesis ')', we're entering a new nested level:
Convert the accumulated digits to an integer (reversing the string first).
Push this new multiplier onto the stack and update
current_multiplier.
For an opening parenthesis '(', we're exiting a nested level:
Divide
current_multiplierby the top value from the stack.
First Pass: Multiplier Calculation (Part 3):
# Store the current multiplier for each character multiplier_at_index[index] = current_multiplier index -= 1For each character, we store the current multiplier and move to the previous character.
Second Pass: Atom Counting (Part 1):
# Second pass: Count atoms atom_map = defaultdict(int) index = 0 while index < formula_length: if formula[index].isupper(): # Start of a new atom start_index = index index += 1 if index < formula_length and formula[index].islower(): index += 1 atom_name = formula[start_index:index]This begins the forward pass to count atoms:
We use a
defaultdictto store atom counts.We identify atoms by their uppercase start and optional lowercase continuation.
Second Pass: Atom Counting (Part 2):
# Get atom count start_index = index while index < formula_length and formula[index].isdigit(): index += 1 atom_count = int(formula[start_index:index] or 1) # Apply pre-calculated multiplier to atom count atom_map[atom_name] += atom_count * multiplier_at_index[index - 1] else: index += 1For each atom:
We parse its count (defaulting to 1 if no count is specified).
We multiply this count by the pre-calculated multiplier for its position.
We add this to the total count for the atom in our
atom_map.
Result Formatting:
# Format the final result formatted_atom_counts = "".join(atom + (str(count) if count > 1 else "") for atom, count in sorted(atom_map.items())) return formatted_atom_countsFinally, we format the result:
We sort the atoms alphabetically.
We create a string where each atom is followed by its count (if greater than 1).
We return this formatted string as the final result.
Complexity Analysis
Time Complexity:
, where is the length of the formula string, and is the number of unique atoms. The two passes through the string (multiplier calculation and atom counting) each take
time. Sorting the unique atoms takes
time. In the worst case where
is proportional to (e.g., each character is a unique atom), the time complexity becomes .
Space Complexity:
, where is the length of the formula string. The
multiplier_at_indexlist requiresspace to store a multiplier for each character. The
atom_mapdictionary can grow up to sizein the worst case where each character is a unique atom. The
multiplier_stackcan also grow up to sizein cases of deeply nested parentheses.
Example
Input:
Step-by-Step Walkthrough:
Initialization:
Set
formula_length = 15(length of the input string)Initialize
multiplier_stack = [1]Initialize
multiplier_at_index = [1] * 15(list of 15 ones)Set
current_multiplier = 1Set
current_count_str = ""
First Pass: Calculate multipliers
Start from the end of the formula (index 14) and move left
Iteration 1 (index 14):
Character: '2'
Update
current_count_strto "2"Store
current_multiplier(1) atmultiplier_at_index[14]
Iteration 2 (index 13):
Character: ')'
Calculate new multiplier: 2
Update
multiplier_stackto [1, 2]Update
current_multiplierto 1 * 2 = 2Reset
current_count_strto ""Store
current_multiplier(2) atmultiplier_at_index[13]
Iterations 3-4 (index 12–11):
Characters: "01"
Update
current_count_strto "10"Store
current_multiplier(2) at both indices
Iteration 5 (index 10):
Character: ')'
Calculate new multiplier: 10
Update
multiplier_stackto [1, 2, 10]Update
current_multiplierto 2 * 10 = 20Reset
current_count_strto ""Store
current_multiplier(20) atmultiplier_at_index[10]
Iterations 6-8 (index 9-7):
Characters: "3OS"
Process digits and reset for alphabets
Store
current_multiplier(20) at all indices
Iteration 9 (index 6):
Character: '('
Update
current_multiplierto 20 // 10 = 2Update
multiplier_stackto [1, 2]Store
current_multiplier(2) atmultiplier_at_index[6]
Iterations 10-11 (index 5-4):
Characters: "NO"
Reset
current_count_strfor alphabetsStore
current_multiplier(2) at both indices
Iteration 12 (index 3):
Character: '('
Update
current_multiplierto 2 // 2 = 1Update
multiplier_stackto [1]Store
current_multiplier(1) atmultiplier_at_index[3]
Iterations 13-15 (index 2–0):
Characters: "32K"
Process digits and reset for alphabet
Store
current_multiplier(1) at all indices
First Pass Summary:
multiplier_at_index = [1, 1, 1, 1, 2, 2, 2, 20, 20, 20, 20, 2, 2, 2, 1]Second Pass: Count atoms
Initialize
atom_map = defaultdict(int)Start from the beginning of the formula (index 0) and move right
Iteration 1 (index 0-2):
Atom: 'K'
Count: 32
Multiplier: 1
Update
atom_map['K'] = 32 * 1 = 32
Iteration 2 (index 4):
Atom: 'O'
Count: 1 (implicit)
Multiplier: 2
Update
atom_map['O'] = 1 * 2 = 2Current state of
atom_map: {'K': 32, 'O': 2}
Iteration 3 (index 5):
Atom: 'N'
Count: 1 (implicit)
Multiplier: 2
Update
atom_map['N'] = 1 * 2 = 2Current state of
atom_map: {'K': 32, 'O': 2, 'N': 2}
Iteration 4 (index 7):
Atom: 'S'
Count: 1 (implicit)
Multiplier: 20
Update
atom_map['S'] = 1 * 20 = 20Current state of
atom_map: {'K': 32, 'O': 2, 'N': 2, 'S': 20}
Iteration 5 (index 8-9):
Atom: 'O'
Count: 3
Multiplier: 20
Update
atom_map['O'] += 3 * 20 = 60Current state of
atom_map: {'K': 32, 'O': 62, 'N': 2, 'S': 20}
Second Pass Summary:
atom_map = {'K': 32, 'O': 62, 'N': 2, 'S': 20}Result Calculation/Final Steps:
Sort the atoms alphabetically: K, N, O, S
For each atom, append its name and count (if > 1) to the result string
Final result: "K32N2O62S20"
Approach 3: Regex Tokenization with Reverse Processing
Understanding the Core Idea
The central concept of this solution is to leverage regular expression (regex) tokenization combined with reverse processing to efficiently count atoms in a complex chemical formula. This approach addresses the challenge of nested parentheses and varying multipliers by tokenizing the formula and then processing these tokens in reverse order.
Regex Tokenization: The solution uses a regular expression to break down the formula into meaningful tokens ( atoms, parentheses, and their associated counts).
Reverse Processing: By processing the tokens from right to left, the solution simplifies the handling of nested structures and multipliers.
Stack for Nested Structures: A stack is used to manage multipliers for nested parentheses, allowing the solution to correctly apply multipliers at different levels of nesting.
Efficient Atom Counting: The reverse processing allows for immediate application of multipliers to atom counts, simplifying the counting process.
Code Walkthrough
Initialization:
multiplier_stack = [1] current_multiplier = 1 atom_map = defaultdict(int)This section initializes key variables:
multiplier_stack: A stack to handle nested structures, initialized with 1 for the base level.current_multiplier: Keeps track of the current multiplier value as we process tokens.atom_map: A defaultdict to store the count of each atom.
Regex Pattern Definition and Tokenization:
# Regex pattern to match atoms, parentheses, and their counts pattern = r"([A-Z][a-z]*)(\d*)|(\()|(\))(\d*)" formula_components = re.findall(pattern, formula) # Process from right to left for correct nested parentheses handling formula_components.reverse()This section defines the regex pattern and tokenizes the formula:
The pattern matches atoms (uppercase followed by optional lowercase), their counts, and parentheses with their multipliers.
([A-Z][a-z]*)(\d*): Matches atoms and their counts.(\()|(\))(\d*): Matches opening and closing parentheses with their multipliers.
re.findall()is used to find all matches in the formula.The resulting list is reversed for right-to-left processing.
Token Processing Loop:
for atom, count, left_parenthesis, right_parenthesis, multiplicity\ in formula_components:This loop iterates through the tokenized and reversed formula components. Each iteration unpacks five possible parts: atom, its count, left parenthesis, right parenthesis, and multiplicity.
Atom Handling:
if atom: # Handle atom and its count atom_count = int(count) if count else 1 atom_map[atom] += current_multiplier * atom_countWhen an atom is encountered:
Its count is determined (defaulting to 1 if not specified).
The atom's count is multiplied by the current multiplier and added to the
atom_map.
Closing Parenthesis Handling:
elif right_parenthesis: # Handle closing parenthesis and its multiplier multiplicity = int(multiplicity) if multiplicity else 1 multiplier_stack.append(multiplicity) current_multiplier *= multiplicityWhen a closing parenthesis is encountered (remember, we're processing in reverse):
Its multiplicity is determined (defaulting to 1 if not specified).
This multiplicity is pushed onto the stack and multiplied into the current multiplier.
Opening Parenthesis Handling:
elif left_parenthesis: # Handle opening parenthesis (end of a group when processing in reverse) current_multiplier //= multiplier_stack.pop()When an opening parenthesis is encountered (end of a group in reverse processing):
The current multiplier is divided by the top value from the stack, effectively ending the nested multiplication.
Result Formatting:
# Format the final result formatted_atom_counts = "".join(atom + (str(count) if count > 1 else "") for atom, count in sorted(atom_map.items())) return formatted_atom_countsFinally, the result is formatted:
Atoms are sorted alphabetically.
Each atom is followed by its count (if greater than 1).
The formatted string is returned as the final result.
Complexity Analysis
Time Complexity:
, where is the length of the formula string, and is the number of unique atoms. The regex matching and reverse processing of tokens take
time. Sorting the unique atoms takes
time. In the worst case where
is proportional to (e.g., each character is a unique atom), the time complexity becomes .
Space Complexity:
, where is the length of the formula string. The space is primarily used by the regex matches list (
formula_components), which can contain up toelements. The
atom_mapdictionary can grow up to sizein the worst case where each character is a unique atom. The
multiplier_stackcan also grow up to sizein cases of deeply nested parentheses.
Example
Input:
Step-by-Step Walkthrough:
Initialization:
Initialize
multiplier_stack = [1]Set
current_multiplier = 1Initialize
atom_map = defaultdict(int)Define regex pattern:
r"([A-Z][a-z]*)(\d*)|(\()|(\))(\d*)"
Tokenization:
Apply regex to formula:
formula_components = [ ('K', '32', '', '', ''), ('', '', '(', '', ''), ('O', '', '', '', ''), ('N', '', '', '', ''), ('', '', '(', '', ''), ('S', '', '', '', ''), ('O', '3', '', '', ''), ('', '', '', ')', '10'), ('', '', '', ')', '2') ]Reverse
formula_components
Process Components:
Start from the end of the formula and move left
Iteration 1:
Component:
('', '', '', ')', '2')Right parenthesis found
Update
multiplier_stackto[1, 2]Update
current_multiplierto 1 * 2 = 2
Iteration 2:
Component:
('', '', '', ')', '10')Right parenthesis found
Update
multiplier_stackto[1, 2, 10]Update
current_multiplierto 2 * 10 = 20
Iteration 3:
Component:
('O', '3', '', '', '')Atom 'O' found with count 3
Update
atom_map['O'] += 20 * 3 = 60
Iteration 4:
Component:
('S', '', '', '', '')Atom 'S' found with implicit count 1
Update
atom_map['S'] += 20 * 1 = 20
Iteration 5:
Component:
('', '', '(', '', '')Left parenthesis found
Update
current_multiplierto 20 // 10 = 2Update
multiplier_stackto[1, 2]
Iteration 6:
Component:
('N', '', '', '', '')Atom 'N' found with implicit count 1
Update
atom_map['N'] += 2 * 1 = 2
Iteration 7:
Component:
('O', '', '', '', '')Atom 'O' found with implicit count 1
Update
atom_map['O'] += 2 * 1 = 2atom_map['O']is now 62
Iteration 8:
Component:
('', '', '(', '', '')Left parenthesis found
Update
current_multiplierto 2 // 2 = 1Update
multiplier_stackto[1]
Iteration 9:
Component:
('K', '32', '', '', '')Atom 'K' found with count 32
Update
atom_map['K'] += 1 * 32 = 32
Processing Summary:
atom_map = {'O': 62, 'S': 20, 'N': 2, 'K': 32}Result Calculation/Final Steps:
Sort the atoms alphabetically: K, N, O, S
For each atom, append its name and count (if > 1) to the result string
Final result: "K32N2O62S20"